题目内容
 水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.
水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.考点:解直角三角形的应用-坡度坡角问题
专题:几何图形问题
分析:先根据两个坡比求出AE和BF的长,然后利用勾股定理求出AD和BC,再由大坝的截面的周长=DC+AD+AE+EF+BF+BC,梯形的面积公式可得出答案.
解答:解:∵迎水坡坡比(DE与AE的长度之比)为1:0.6,DE=30m,
∴AE=18米,
在RT△ADE中,AD=
=6
米
∵背水坡坡比为1:2,
∴BF=60米,
在RT△BCF中,BC=
=30
米,
∴周长=DC+AD+AE+EF+BF+BC=6
+10+30
+88=(6
+30
+98)米,
面积=(10+18+10+60)×30÷2=1470(平方米).
故大坝的截面的周长是(6
+30
+98)米,面积是1470平方米.
∴AE=18米,
在RT△ADE中,AD=
| DE2+AE2 |
| 34 |
∵背水坡坡比为1:2,
∴BF=60米,
在RT△BCF中,BC=
| CF2+BF2 |
| 5 |
∴周长=DC+AD+AE+EF+BF+BC=6
| 34 |
| 5 |
| 34 |
| 5 |
面积=(10+18+10+60)×30÷2=1470(平方米).
故大坝的截面的周长是(6
| 34 |
| 5 |
点评:本题考查了坡度和坡比问题,利用三角函数求得梯形的各边,还涉及了勾股定理的应用,解答本题关键是理解坡比所表示的意义.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
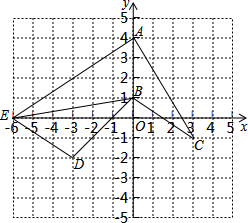 已知A,B,C,D,E各点的坐标如图,请分别求出△ABC、△EAB和△BDE的面积.
已知A,B,C,D,E各点的坐标如图,请分别求出△ABC、△EAB和△BDE的面积.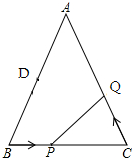 如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动. 如图,点C是直线MN上一点,CA⊥CB,且CA=CB,过A、B分别作MN的垂线,垂足分别为E、F,试判断线段AE、BF与EF有什么数量关系,并证明你的结论.
如图,点C是直线MN上一点,CA⊥CB,且CA=CB,过A、B分别作MN的垂线,垂足分别为E、F,试判断线段AE、BF与EF有什么数量关系,并证明你的结论.