题目内容
 如图,点C是直线MN上一点,CA⊥CB,且CA=CB,过A、B分别作MN的垂线,垂足分别为E、F,试判断线段AE、BF与EF有什么数量关系,并证明你的结论.
如图,点C是直线MN上一点,CA⊥CB,且CA=CB,过A、B分别作MN的垂线,垂足分别为E、F,试判断线段AE、BF与EF有什么数量关系,并证明你的结论.考点:全等三角形的判定与性质,等腰直角三角形
专题:几何图形问题
分析:证得△AEC≌△CFB(AAS),得到AE=CF,EC=FB,即得AE+BF=EF,由此推理论证即可.
解答:答:AE+BF=EF.
证明:∵∠EAC+∠ACE=90°,∠ACE+∠BCF=90°,
∴∠EAC=∠FCB,
又∵AE⊥MN、BF⊥MN,垂足分别为E、F,
∴∠AEC=∠CFB=90°,
且AC=BC,
在△AEC和△CFB中,
∴△AEC≌△CFB(AAS).
∴AE=CF,EC=FB.
∴EF=AE+BF.
故线段AE与BF之和等于线段EF.
证明:∵∠EAC+∠ACE=90°,∠ACE+∠BCF=90°,
∴∠EAC=∠FCB,
又∵AE⊥MN、BF⊥MN,垂足分别为E、F,
∴∠AEC=∠CFB=90°,
且AC=BC,
在△AEC和△CFB中,
|
∴△AEC≌△CFB(AAS).
∴AE=CF,EC=FB.
∴EF=AE+BF.
故线段AE与BF之和等于线段EF.
点评:本题主要考查三角形全等的判定,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
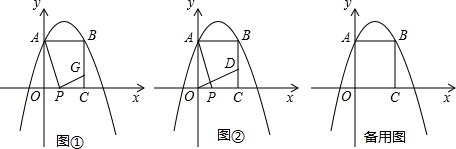
 水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.
水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.

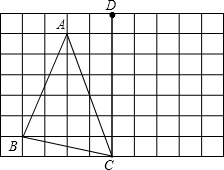 如图,每个小正方形的边长都等于1,△ABC的三个顶点都在格点(小正方形的顶点)上.
如图,每个小正方形的边长都等于1,△ABC的三个顶点都在格点(小正方形的顶点)上.