题目内容
【题目】如图,点![]() 都在反比例函数
都在反比例函数![]() 的图象上.
的图象上.
(1)求![]() 的值;
的值;
(2)如果![]() 为
为![]() 轴上一点,
轴上一点,![]() 为
为![]() 轴上一点,以点
轴上一点,以点![]() 为顶点的四边形是平行四边形,试求直线
为顶点的四边形是平行四边形,试求直线![]() 的函数表达式;
的函数表达式;
(3)将线段![]() 沿直线
沿直线![]() 进行对折得到线段
进行对折得到线段![]() ,且点
,且点![]() 始终在直线
始终在直线![]() 上,当线段
上,当线段![]() 与
与![]() 轴有交点时,则
轴有交点时,则![]() 的取值范围为_______(直接写出答案)
的取值范围为_______(直接写出答案)

【答案】(1)m=3,k=12;(2)y![]() x+2或y
x+2或y![]() x﹣2;(3)
x﹣2;(3)![]() .
.
【解析】
(1)由题可得m(m+1)=(m+3)(m﹣1)=k,解这个方程就可求出m、k的值.
(2)由于点A、点B是定点,可对线段AB进行分类讨论:AB是平行四边形的边、AB是平行四边形的对角线,再利用平行四边形的性质、中点坐标公式及直线的相关知识就可解决问题.
(3)由于点A关于直线y=kx+b的对称点点A1始终在直线OA上,因此直线y=kx+b必与直线OA垂直,只需考虑两个临界位置(A1在x轴上、B1在x轴上)对应的b的值,就可以求出b的取值范围.
(1)∵点A(m,m+1),B(m+3,m﹣1)都在反比例函数y![]() 的图象上,∴m(m+1)=(m+3)(m﹣1)=k.
的图象上,∴m(m+1)=(m+3)(m﹣1)=k.
解得:m=3,k=12,∴m、k的值分别为3、12.
(2)设点M的坐标为(m,0),点N的坐标为(O,n).
①若AB为平行四边形的一边.
Ⅰ.点M在x轴的正半轴,点N在y轴的正半轴,连接BN、AM交于点E,连接AN、BM,如图1.
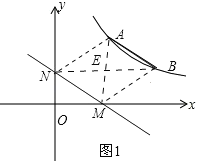
∵四边形ABMN是平行四边形,∴AE=ME,NE=BE.
∵A(3,4)、B(6,2)、M(m,0)、N(0,n),∴由中点坐标公式可得:
xE![]() ,yE
,yE![]() ,∴m=3,n=2,∴M(3,0)、N(0,2).
,∴m=3,n=2,∴M(3,0)、N(0,2).
设直线MN的解析式为y=kx+b.
则有![]()
解得: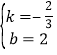 ,∴直线MN的解析式为y
,∴直线MN的解析式为y![]() x+2.
x+2.
Ⅱ.点M在x轴的负半轴,点N在y轴的负半轴,连接BM、AN交于点E,连接AM、BN,如图2,同理可得:直线MN的解析式为y![]() x﹣2.
x﹣2.
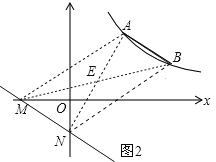
②若AB为平行四边形的一条对角线,连接AN、BM,设AB与MN交于点F,如图3.
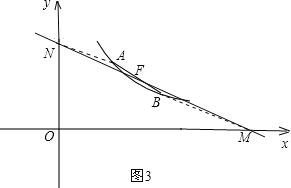
同理可得:直线MN的解析式为y![]() x+6,此时点A、B都在直线MN上,故舍去.
x+6,此时点A、B都在直线MN上,故舍去.
综上所述:直线MN的解析式为y![]() x+2或y
x+2或y![]() x﹣2.
x﹣2.
(3)①当点B1落到x轴上时,如图4.
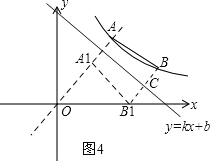
设直线OA的解析式为y=ax.
∵点A的坐标为(3,4),∴3a=4,即a![]() ,∴直线OA的解析式为y
,∴直线OA的解析式为y![]() x.
x.
∵点A1始终在直线OA上,∴直线y=kx+b与直线OA垂直,∴![]() k=﹣1,∴k
k=﹣1,∴k![]() .
.
由于BB1∥OA,因此直线BB1可设为y![]() x+c.
x+c.
∵点B的坐标为(6,2),∴![]() 6+c=2,即c=﹣6,∴直线BB1解析式为y
6+c=2,即c=﹣6,∴直线BB1解析式为y![]() x﹣6.
x﹣6.
当y=0时,![]() x﹣6=0.则有x
x﹣6=0.则有x![]() ,∴点B1的坐标为(
,∴点B1的坐标为(![]() ,0).
,0).
∵点C是BB1的中点,∴点C的坐标为(![]() )即(
)即(![]() ,1).
,1).
∵点C在直线y![]() x+b上,∴
x+b上,∴![]() b=1.
b=1.
解得:b![]() .
.
②当点A1落到x轴上时,如图5.
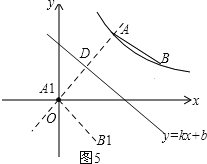
此时,点A1与点O重合.
∵点D是AA1的中点,A(3,4),A1(0,0),∴D(![]() ,2).
,2).
∵点D在直线y![]() x+b上,∴
x+b上,∴![]() b=2.
b=2.
解得:b![]() .
.
综上所述:当线段A1B1与x轴有交点时,则b的取值范围为![]() .
.
故答案为:![]() .
.

 53随堂测系列答案
53随堂测系列答案