题目内容
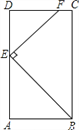
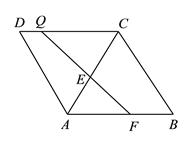
【题目】已知:∠A=(90+x)°,∠B=(90﹣x)°,∠CED=90°,射线EF∥AC,2∠C﹣∠D=m.(1)判断AC与BD的位置关系,并说明理由.
(2)如图1,当m=30°时,求∠C、∠D的度数.
(3)如图2,求∠C、∠D的度数(用含m的代数式表示).
【答案】(1)AC∥BD,理由见解析;(2)∠C=40°,∠D=50°;(3)∠C=90°+m,∠D=180°+m
【解析】
(1)根据同旁内角互补两直线平行求出AC∥BD;
(2)根据两直线平行,内错角相等可得∠CEF=∠C,∠DEF=∠D,然后列出关于∠C、∠D的二元一次方程组求解即可;
(3)根据两直线平行,内错角相等可得∠CEF=∠C,∠DEF=∠D,再根据∠CED=∠DEF-∠CEF得到∠D-∠C=90°,然后求解即可.
(1)∵∠A+∠B=(90+x)°+(90x)°=180°,
∴AC∥BD
(2)∵EF∥AC,
∴AC∥EF∥BD,
∴∠CEF=∠C,∠DEF=∠D,
∵∠CED=90,
∴∠C+∠D=90,
联立
![]() ,
,
解得![]()
(3)∵EF∥AC,
∴AC∥EF∥BD,
∴∠CEF=∠C,∠DEF=∠D,
∵∠CED=∠DEF-∠CEF=90°,
∴∠D-∠C=90°,①
又2∠C∠D=m ②
联立,① ②
解得∠C=90°+m,∠D=180°+m

练习册系列答案
相关题目