题目内容
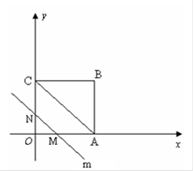
如图,在△ABC中,AB=AC,tan∠B=2, BC=3 . 边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°. 设BE=x, MN=y,则能表示y与x的函数关系的大致图象是( )
. 边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°. 设BE=x, MN=y,则能表示y与x的函数关系的大致图象是( )

 . 边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°. 设BE=x, MN=y,则能表示y与x的函数关系的大致图象是( )
. 边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°. 设BE=x, MN=y,则能表示y与x的函数关系的大致图象是( )
A. |
B. |
C. |
D. |
D.
试题分析:分两种情况讨论;
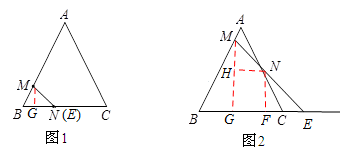
①当点N在边BC时,点E N重合,如图1,此时
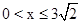 .
.过点M作MG⊥BC于点G,
∵∠MNG=45°,∴MG=GN=
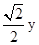 .
.∵tan∠B=2,∴BG=
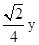 .
.∴
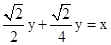 ,即
,即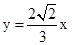 .
.②当点N在BC延长线上时,如图2,此时
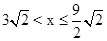 .
.过点M作MG⊥BC于点G,过点N作NF⊥BC于点F,过点N作NH⊥MG于点H,
设NE=a,
∵∠MEG=45°,HN∥BC,∴MH=HN=
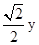 ,NF=FE=
,NF=FE=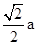 ,MG=GE=
,MG=GE=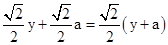 .
.∵AB=AC,tan∠B=2,∴tan∠NCF="2." ∴FC=
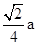 .
.又∵tan∠B=2,∴BG=
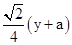 .
.∵BC=BG+GF+FC,GF=HN,∴
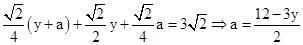 .
.∴FE=
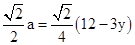 ,BG=
,BG=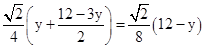 .
.∴
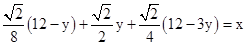 ,即
,即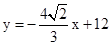 .
.综上所述,y与x的函数关系为
 .
.故选D.

练习册系列答案
相关题目
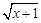 可中,自变量x的取值范围是 .
可中,自变量x的取值范围是 .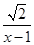 中,自变量x的取值范围是
中,自变量x的取值范围是