题目内容
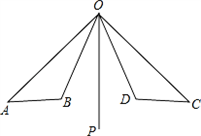
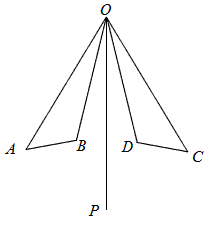
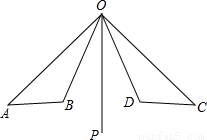
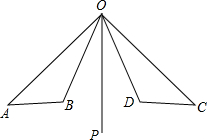 已知:如图,OP是∠AOC和∠BOD的平分线,OA=OC,OB=OD.
已知:如图,OP是∠AOC和∠BOD的平分线,OA=OC,OB=OD.试说明:AB=CD.
解:∵OP是∠AOC和∠BOD的平分线
∴∠AOP=
∴∠AOP-∠BOP=∠COP-∠DOP
即∠
在△ABO和△CDO中
|
∴
∴
分析:根据角平分线的定义以及等式的性质即可解答.
解答:解:∵OP是∠AOC和∠BOD的平分线,
∴∠AOP=∠COP,∠BOP=∠DOP,
∴∠AOP-∠BOP=∠COP-∠DOP,
即∠AOB=∠COD.
在△ABO和△CDO中,
,
∴△AOB≌△COD ( SAS),
∴AB=CD (全等三角形的对应边相等).
∴∠AOP=∠COP,∠BOP=∠DOP,
∴∠AOP-∠BOP=∠COP-∠DOP,
即∠AOB=∠COD.
在△ABO和△CDO中,
|
∴△AOB≌△COD ( SAS),
∴AB=CD (全等三角形的对应边相等).
点评:本题考查了三角形全等的判定与性质,正确理解角平分线的定义以及等式的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目