题目内容
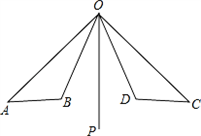
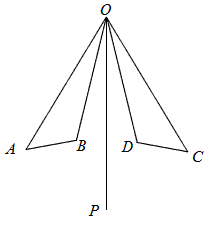
已知:如图,OP是∠AOC和∠BOD的平分线,OA=OC,OB=OD.求证:AB=CD.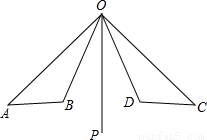
【答案】分析:根据角平分线的性质得出∠AOP=∠COP,∠BOP=∠DOP,从而推出∠AOB=∠COD,再利用SAS判定其全等从而得到AB=CD.
解答:证明:∵OP是∠AOC和∠BOD的平分线,
∴∠AOP=∠COP,∠BOP=∠DOP.
∴∠AOB=∠COD.
在△AOB和△COD中,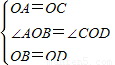 .
.
∴△AOB≌△COD.
∴AB=CD.
点评:本题考查三角形全等的判定方法,以及全等三角形的性质.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.本题比较简单,读已知时就能想到要用全等来证明线段相等.
解答:证明:∵OP是∠AOC和∠BOD的平分线,
∴∠AOP=∠COP,∠BOP=∠DOP.
∴∠AOB=∠COD.
在△AOB和△COD中,
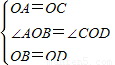 .
.∴△AOB≌△COD.
∴AB=CD.
点评:本题考查三角形全等的判定方法,以及全等三角形的性质.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.本题比较简单,读已知时就能想到要用全等来证明线段相等.

练习册系列答案
相关题目
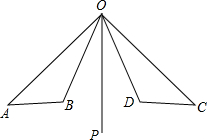 已知:如图,OP是∠AOC和∠BOD的平分线,OA=OC,OB=OD.
已知:如图,OP是∠AOC和∠BOD的平分线,OA=OC,OB=OD.