题目内容
【题目】为了迎接“五一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:已知:用3600元购进甲种运动鞋的数量与用3000元购进乙种运动鞋的数量相同.
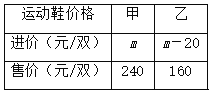
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21600元,且不超过22440元,问该专卖店有多少种进货方案?
【答案】(1) m=120;(2)15种.
【解析】试题分析:(1)用总价除以单价表示出购进鞋的数量,根据两种鞋的数量相等列出方程求解即可;
(2)设购进甲种运动鞋x双,表示出乙种运动鞋(200-x)双,然后根据总利润列出一元一次不等式,求出不等式组的解集后,再根据鞋的双数是正整数解答即可.
试题解析:(1)依题意得
![]() ,
,
整理得,3600(m-2)=3000m,
解得m=120,
经检验,m=120是原分式方程的解,
所以,m=120;
(2)设购进甲种运动鞋x双,则乙种运动鞋(200-x)双,
根据题意得,
 ,
,
不等式组的解集是160≤x≤174,
∵x是正整数,174-160+1=15,
∴共有15种方案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目