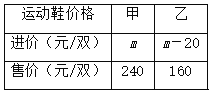
��Ŀ����
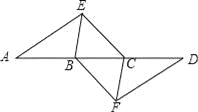
����Ŀ����ͼ�����ı���ABCD���ĸ�����ֱ����Խ���AC��BD��ƽ���ߣ���Χ�ɵ��ı���EFGH��Ȼ��ƽ���ı��Σ�
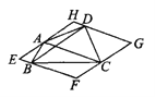
(1)���ı���ABCD�ֱ������Ρ����Ρ�ƽ���ı���ʱ����Ӧ���ı���EFGHһ���ǡ�ƽ���ı��Ρ����Ρ����Ρ������Ρ��е���һ�֣��뽫��Ľ��������±���

(2)��֮����������������Χ�ɵ�ƽ���ı���EFGH�ֱ��Ǿ��Ρ�����ʱ����Ӧ��ԭ�ı���ABCD��������������������
�� ʱ���ı���EFGH�Ǿ��Σ��� ʱ�ı���EFGH������.
���𰸡���1�����Σ����Σ�ƽ���ı��Σ���2���Խ����ഹֱ��AC��BD�����Խ�����ȣ�AC=BD��.
�������������������1��ԭ�ı���������ʱ�����εĶԽ����ഹֱ�����ƽ���ı���Ӧ���Ǹ����Σ�ƽ���ı������ڵ����߶���ֱ����
ԭ�ı����Ǿ��λ��������ʱ�����ĶԽ�����ȣ���ôƽ���ı���Ӧ���Ǹ����Σ�ƽ���ı������ڵ����߶���ȣ���
ԭ�ı�����ƽ���ı���ʱ���е����߹��ɵ��ı����ǶԽ�����ȵ�ƽ���ı���.
��2�����ݣ�1�����ǿɿ���Ҫ��ʹ�ó���ƽ���ı����Ǿ��Σ���ôԭ�ı��εĶԽ��߾ͱ��봹ֱ����Ϊֻ������ƽ���ı��ε��������߲Ŵ�ֱ��ͬ��ƽ���ı���������ʱ��ԭ�ı��εĶԽ��߾ͱ�����ȣ�
�����������1�����Σ� ���Σ� ƽ���ı��Σ�
��2���Խ����ഹֱ��AC��BD�����Խ�����ȣ�AC=BD����