Question

【题目】我们给出如下定义，如果一个四边形有一条对角线能将其分成一个等边三角形和一个直角三角形，那么这个四边形叫做等垂四边形，这条对角线叫做这个四边形的等垂对角线.

（1）已知是四边形的等垂对角线，，均为钝角，且比大，那么________.

（2）如图，已知与关于直线对称，、两点分别在、边上，，，.求证：四边形是等垂四边形。

Answer 1

【答案】（1）110°或150°；（2）见解析.

【解析】

（1）由题意分∠D=90°与∠DCA=90°两种情况，并利用四边形内角和定理求解即可；

（2）连接，先利用SAS证明，再证明是等边三角形，最后利用勾股定理的逆定理证明是直角三角形即可.

解：（1）或.

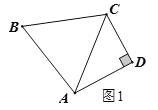
如图1，当∠D=90°时，设=x°，则=(x－10)°，根据四边形内角和定理可得：

x+x－10+90+60=360，解得x=110，即110°；

如图2，当∠DCA=90°时，60°+90°=150°；

故答案为或.

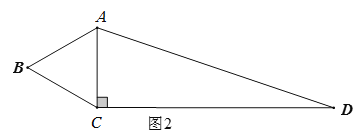
（2）证明：如图3，连接.

∵和关于对称，

∴，，

又∵，

∴，

∴，

∵，

∴是等边三角形，

∴，

又∵，

∴，

∴，

∴是直角三角形，

∴四边形是等垂四边形.