��Ŀ����
����Ŀ��![]() �У�
�� ![]() ����
����![]() �ֱ��ڱ�
�ֱ��ڱ�![]() �ϣ���
�ϣ���![]() �����
�����![]() ����
����![]() �غϣ���
�غϣ���![]() ����
����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת�õ�
˳ʱ����ת�õ�![]() ��
��
��1������![]() ��
��![]() ��ʱ������
��ʱ������![]() ��
��
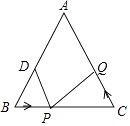
����ͼ1�� ![]() ���߶�
���߶�![]() ��λ�ù�ϵ��_____________��
��λ�ù�ϵ��_____________��
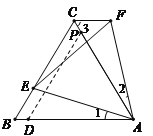
����ͼ2�� ![]() ����ʱ
����ʱ![]() ��������е�λ�ù�ϵ�������㣬��֤����Ľ��ۣ��������㣬��˵�����ɣ�
��������е�λ�ù�ϵ�������㣬��֤����Ľ��ۣ��������㣬��˵�����ɣ�
��2����![]() ����
����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת�����У���
˳ʱ����ת�����У���![]() ��һ����������
��һ����������![]() ��ʱ������
��ʱ������![]() ����ʱ
����ʱ![]() �����㣨1�����е�λ�ù�ϵ�������㣬��֤����Ľ��ۣ���ֱ��д��
�����㣨1�����е�λ�ù�ϵ�������㣬��֤����Ľ��ۣ���ֱ��д��![]() ��ȡֵ��Χ���ú�
��ȡֵ��Χ���ú�![]() ��ʽ�ӱ�ʾ�����������㣬��˵�����ɣ�
��ʽ�ӱ�ʾ�����������㣬��˵�����ɣ�

���𰸡���1����ƽ��![]() �������㣨��
�������㣨��![]() �������ɼ�������
�������ɼ�������
��2�����㣨��![]() ����
����
��![]() ʱ��
ʱ�� ![]() ��
��
��![]() ʱ��
ʱ�� ![]()
����![]() ��
��
�������������������1������![]() ��
��![]() ,
, ![]() ��
�� ![]() ��
��![]() ,�ɴ�
,�ɴ�![]() ��
��![]() ��
��![]() =
=![]() ,�ɵ�
,�ɵ�![]() .
.
����![]() ��
�� ![]() ��
��![]() �ǵȱ������Σ���
�ǵȱ������Σ���![]() �ǵȱ������Σ�
�ǵȱ������Σ� ![]() ���ɱ߽DZ߿�֤
���ɱ߽DZ߿�֤![]() ��
��![]() ����ȫ�������ζ�Ӧ����ȣ������ڴ��ǣ���֤
����ȫ�������ζ�Ӧ����ȣ������ڴ��ǣ���֤![]() ��
��
��2��![]() ��
�� ![]() ʱ����
ʱ����![]() ��
��![]() ��
��![]() ����
����![]()
��![]() ��
��![]() ������
������![]() ����
����![]() ��ͬ����֤
��ͬ����֤![]() .
.
�����������1����ƽ��![]()
���ɣ���![]() ��
�� ![]() ��
��
��![]()
![]() ��
��
![]() ��
��![]() ,
,
![]() ��
�� ![]() ��
��![]() ,
, ![]()
��![]() ��
��![]() ,
,
��![]() ,
,
��![]() ��
��![]() ,
,
��![]() ��
��
![]() ,
,
��![]() ;
;
�����㣨��![]() ��
��
�������£�
��![]() ��
�� ![]()
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() ��
�� ![]()
�֡�![]() ��
��
��![]()
��![]() �ǵȱ�������
�ǵȱ�������
![]() ��
�� ![]() ��
��![]() ��
�� ![]() ��
��
��![]()
��![]() ��
��![]() ��
�У� 
��![]() ��
��![]()
��![]()
��![]()
��![]()
��2�����㣨��![]() ��
��
�������£� ![]()
��![]() ��
��![]() ��
��![]() ��
��![]()
��![]() ��
��![]() ��
��![]()
�ɣ�2��֪![]()
��![]() ��
��![]() ��
��![]()
�֡�![]() ��
��![]()
��![]() ��
��![]()
��ʱ�� ![]() ����
����![]() ��
��
�ڵ�![]() ��ͬ����֤
��ͬ����֤![]() ��ʱ
��ʱ![]()
������������![]() ʱ��
ʱ�� ![]()
��![]() ʱ��
ʱ��
![]() ����
����![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�