题目内容
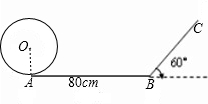
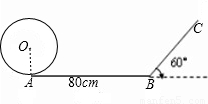
一位小朋友在不打滑的平面轨道上滚动一个半径为10cm的圆盘，当滚到与坡面BC开始相切时停止．其中AB=80cm，BC与水平面的夹角为60度．
（1）求出圆盘在AB上滚动一圈，其圆心所经过的路线的长度（精确到0.1cm）；
（2）当圆盘从A点滚到与BC开始相切时停止，其圆心所经过的路线长是多少（精确到0.1cm）．
解：（1）∵圆盘在AB上滚动一圈，其圆心所经过的路线的长度，就是等于圆的周长，而圆盘半径为10cm，
∴圆心经过的路线的长度是20π≈62.8cm；
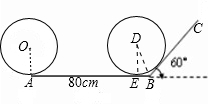
（2）如图，当圆转动到与BC相切，停止的位置设是圆D，与AB切于E，连接DE，DB，则DE⊥AB，
在直角△DEB中，BE=DE•tan30°=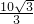
≈5.8cm，
AB-BE=80-5.8=74.2（cm）
∴圆心经过的路线长约是74.2cm．
分析：（1）圆盘在AB上滚动一圈，其圆心所经过的路线的长度，就是等于圆的周长，根据圆周长的公式求出求出；
（2）当圆与BC相切时，圆与AB，BC都相切且∠ABC=120°，在直角△DEB中，可以求出BE，则圆心转过的路线是AE，在直角三角形DEB中根据已知条件求出BE就可以求出AE．
点评：本题主要考查了切线的性质，切线长定理及利用三角函数解直角三角形等知识，有一定的综合性．
∴圆心经过的路线的长度是20π≈62.8cm；
（2）如图，当圆转动到与BC相切，停止的位置设是圆D，与AB切于E，连接DE，DB，则DE⊥AB，
在直角△DEB中，BE=DE•tan30°=
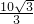≈5.8cm，AB-BE=80-5.8=74.2（cm）
∴圆心经过的路线长约是74.2cm．
分析：（1）圆盘在AB上滚动一圈，其圆心所经过的路线的长度，就是等于圆的周长，根据圆周长的公式求出求出；
（2）当圆与BC相切时，圆与AB，BC都相切且∠ABC=120°，在直角△DEB中，可以求出BE，则圆心转过的路线是AE，在直角三角形DEB中根据已知条件求出BE就可以求出AE．
点评：本题主要考查了切线的性质，切线长定理及利用三角函数解直角三角形等知识，有一定的综合性．
练习册系列答案
相关题目
