题目内容
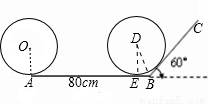
(2008•南安市质检)一位小朋友在不打滑的平面轨道上滚动一个半径为10cm的圆盘,当滚到与坡面BC开始相切时停止.其中AB=80cm,BC与水平面的夹角为60度.(1)求出圆盘在AB上滚动一圈,其圆心所经过的路线的长度(精确到0.1cm);
(2)当圆盘从A点滚到与BC开始相切时停止,其圆心所经过的路线长是多少(精确到0.1cm).

【答案】分析:(1)圆盘在AB上滚动一圈,其圆心所经过的路线的长度,就是等于圆的周长,根据圆周长的公式求出求出;
(2)当圆与BC相切时,圆与AB,BC都相切且∠ABC=120°,在直角△DEB中,可以求出BE,则圆心转过的路线是AE,在直角三角形DEB中根据已知条件求出BE就可以求出AE.
解答:解:(1)∵圆盘在AB上滚动一圈,其圆心所经过的路线的长度,就是等于圆的周长,而圆盘半径为10cm,
∴圆心经过的路线的长度是20π≈62.8cm;
(2)如图,当圆转动到与BC相切,停止的位置设是圆D,与AB切于E,连接DE,DB,则DE⊥AB,
在直角△DEB中,BE=DE•tan30°=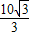 ≈5.8cm,
≈5.8cm,
AB-BE=80-5.8=74.2(cm)
∴圆心经过的路线长约是74.2cm.
点评:本题主要考查了切线的性质,切线长定理及利用三角函数解直角三角形等知识,有一定的综合性.
(2)当圆与BC相切时,圆与AB,BC都相切且∠ABC=120°,在直角△DEB中,可以求出BE,则圆心转过的路线是AE,在直角三角形DEB中根据已知条件求出BE就可以求出AE.
解答:解:(1)∵圆盘在AB上滚动一圈,其圆心所经过的路线的长度,就是等于圆的周长,而圆盘半径为10cm,
∴圆心经过的路线的长度是20π≈62.8cm;
(2)如图,当圆转动到与BC相切,停止的位置设是圆D,与AB切于E,连接DE,DB,则DE⊥AB,
在直角△DEB中,BE=DE•tan30°=
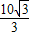 ≈5.8cm,
≈5.8cm,AB-BE=80-5.8=74.2(cm)
∴圆心经过的路线长约是74.2cm.

点评:本题主要考查了切线的性质,切线长定理及利用三角函数解直角三角形等知识,有一定的综合性.

练习册系列答案
相关题目
(2008•南安市质检)某中学为了解全校2000名学生参加课外锻炼的情况,从中抽查50名学生一周内平均每天参加课外锻炼的时间(单位为分钟,且取整数)将抽查得到的数据进行适当整理,分成5组,列出了下面尚未完成的频率分布表:
(1)直接写出表中欠缺的数据x、y的值:x=______,y=______.
(2)由本次抽查结果估计这所学校约有多少名学生平均每天参加课外锻炼的时间多于40分钟?
| 分组 | 10.5-20.5 | 20.5-30.5 | 30.5-40.5 | 40.5-50.5 | 50.5-60.5 | 合计 |
| 频数 | 5 | 11 | 20 | x | 2 | 50 |
| 频率 | 0.10 | y | 0.40 | 0.24 | 0.04 | 1.00 |
(2)由本次抽查结果估计这所学校约有多少名学生平均每天参加课外锻炼的时间多于40分钟?


 -(π-1)+(
-(π-1)+( )-1.
)-1.