题目内容
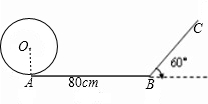
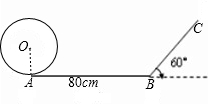
一位小朋友在不打滑的平面轨道上滚动一个半径为5cm的圆环，当滚到与坡面BC开始相切时停止．其AB=40cm，BC与水平面的夹角为60°．其圆心所经过的路线长是 cm（结果保留根号）．
【答案】分析：先作图，连接OD、BD，作DE⊥AB，可证得∠DBE=60°，再由勾股定理求得BE，则圆心所经过的路线长AB-BE．
解答：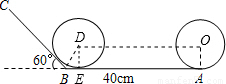
解：连接OD、BD，作DE⊥AB，
∵BC与水平面的夹角为60°，
∴∠DBE=60°，
∴∠BDE=30°，
设BE=x，则BD=2x，
∴由勾股定理得4x2-x2=25，
解得x=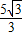
，
∴OD=AE=40-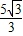
，
故答案为40-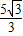
．
点评：本题考查了切线长定理，勾股定理，将圆心所移动的距离转化为AE的长，是解题的关键．
解答：
解：连接OD、BD，作DE⊥AB，∵BC与水平面的夹角为60°，
∴∠DBE=60°，
∴∠BDE=30°，
设BE=x，则BD=2x，
∴由勾股定理得4x2-x2=25，
解得x=
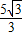，∴OD=AE=40-
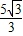，故答案为40-
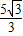．点评：本题考查了切线长定理，勾股定理，将圆心所移动的距离转化为AE的长，是解题的关键．
练习册系列答案
相关题目
