题目内容
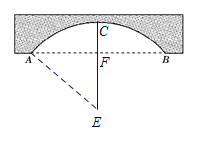
【题目】如图,一拱形公路桥,圆弧形桥拱的水面跨度AB=80 m,桥拱到水面的最大高度为20 m.(1)求桥拱的半径.
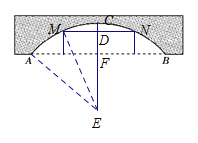
(2)现有一艘宽60 m,顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.

【答案】(1) 桥拱的半径为50 m;(2)这艘轮船能顺利通过,理由见解析.
【解析】试题分析:
(1)找到圆的圆心E,过点E作EF⊥AB于点F,延长EF交![]() 于点C,连接AE,在Rt△AEF中用勾股定理求AE的长;
于点C,连接AE,在Rt△AEF中用勾股定理求AE的长;
(2)连接EM,设EC与MN的交点为D,在Rt△DME中,用勾股定理求出DE,再求DF的长,比较DF与9的大小,即可求解.
试题解析:
(1)如图,点E是桥拱所在圆的圆心.过点E作EF⊥AB于点F,
延长EF交![]() 于点C,连接AE,则CF=20 m.由垂径定理知,F是AB的中点,
于点C,连接AE,则CF=20 m.由垂径定理知,F是AB的中点,
∴AF=FB=![]() AB=40 m.设半径是r m,由勾股定理,得AE2=AF2+EF2=AF2+(CE-CF)2,即r2=402+(r-20)2.解得r=50.∴桥拱的半径为50 m.
AB=40 m.设半径是r m,由勾股定理,得AE2=AF2+EF2=AF2+(CE-CF)2,即r2=402+(r-20)2.解得r=50.∴桥拱的半径为50 m.
(2)这艘轮船能顺利通过.理由如下:
当宽60 m的轮船刚好可通过拱桥时,如图,MN为轮船顶部的位置.
连接EM,设EC与MN的交点为D,
则DE⊥MN,∴DM=30 m,∴DE=![]() =
=![]() =40(m).
=40(m).
∵EF=EC-CF=50-20=30(m),∴DF=DE-EF=40-30=10(m).
∵10 m>9 m,∴这艘轮船能顺利通过.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目