题目内容
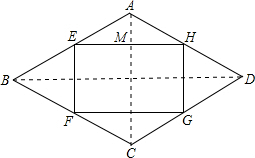
(2013•莆田)如图所示,某学校拟建一个含内接矩形的菱形花坛(花坛为轴对称图形).矩形的四个顶点分别在菱形四条边上,菱形ABCD的边长AB=4米,∠ABC=60°.设AE=x米(0<x<4),矩形EFGH的面积为S米2.
(1)求S与x的函数关系式;
(2)学校准备在矩形内种植红色花草,四个三角形内种植黄色花草.已知红色花草的价格为20元/米2,黄色花草的价格为40元/米2.当x为何值时,购买花草所需的总费用最低,并求出最低总费用(结果保留根号)?

(1)求S与x的函数关系式;
(2)学校准备在矩形内种植红色花草,四个三角形内种植黄色花草.已知红色花草的价格为20元/米2,黄色花草的价格为40元/米2.当x为何值时,购买花草所需的总费用最低,并求出最低总费用(结果保留根号)?

分析:(1)连接AC、BD,根据轴对称的性质,可得EH∥BD,EF∥AC,△BEF为等边三角形,从而求出EF,在Rt△AEM中求出EM,继而得出EH,这样即可得出S与x的函数关系式.
(2)根据(1)的答案,可求出四个三角形的面积,设费用为W,则可得出W关于x的二次函数关系式,利用配方法求最值即可.
(2)根据(1)的答案,可求出四个三角形的面积,设费用为W,则可得出W关于x的二次函数关系式,利用配方法求最值即可.
解答:解:(1)连接AC、BD,
∵花坛为轴对称图形,
∴EH∥BD,EF∥AC,
∴△BEF∽△BAC,
∵四边形ABCD是菱形,
∴AB=AC,
又∵∠ABC=60°,
∴△ABC是等边三角形.
同理,得到△BEF是等边三角形,
∴EF=BE=AB-AE=4-x,
在Rt△AEM中,∠AEM=∠ABD=30°,
则EM=AEcos∠AEM=
x,
∴EH=2EM=
x,
故可得S=(4-x)×
x=-
x2+4
x.
(2)易求得菱形ABCD的面积为8
m2,
由(1)得,矩形ABCD的面积S=-
x2+4
x.
则可得四个三角形的面积为(8
+
x2-4
x),
设总费用为W,
则W=20(-
x2+4
x)+40(8
+
x2-4
x)
=20
x2-80
x+320
=20
(x-2)2+240
,
∵0<x<4,
∴当x=2时,W取得最小,W最小=240
元.
即当x为2时,购买花草所需的总费用最低,最低费用为240
元.

∵花坛为轴对称图形,
∴EH∥BD,EF∥AC,
∴△BEF∽△BAC,
∵四边形ABCD是菱形,
∴AB=AC,
又∵∠ABC=60°,
∴△ABC是等边三角形.
同理,得到△BEF是等边三角形,
∴EF=BE=AB-AE=4-x,
在Rt△AEM中,∠AEM=∠ABD=30°,
则EM=AEcos∠AEM=
| ||
| 2 |
∴EH=2EM=
| 3 |
故可得S=(4-x)×
| 3 |
| 3 |
| 3 |
(2)易求得菱形ABCD的面积为8
| 3 |
由(1)得,矩形ABCD的面积S=-
| 3 |
| 3 |
则可得四个三角形的面积为(8
| 3 |
| 3 |
| 3 |
设总费用为W,
则W=20(-
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
=20
| 3 |
| 3 |
| 3 |
=20
| 3 |
| 3 |
∵0<x<4,
∴当x=2时,W取得最小,W最小=240
| 3 |
即当x为2时,购买花草所需的总费用最低,最低费用为240
| 3 |
点评:本题考查了二次函数的应用,首先需要根据花坛为轴对称图形,得出EH∥BD,EF∥AC,重点在于分别得出EF、EH关于x的表达式,另外要掌握配方法求二次函数最值的应用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 (2013•莆田)如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )
(2013•莆田)如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )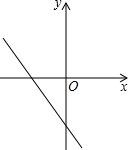 (2013•莆田)如图,一次函数y=(m-2)x-1的图象经过二、三、四象限,则m的取值范围是( )
(2013•莆田)如图,一次函数y=(m-2)x-1的图象经过二、三、四象限,则m的取值范围是( )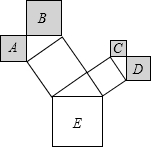 (2013•莆田)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为2,5,1,2.则最大的正方形E的面积是
(2013•莆田)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为2,5,1,2.则最大的正方形E的面积是 (2013•莆田)如图,抛物线y=ax2+bx+c的开口向下,与x轴交于点A(-3,0)和点B(1,0).与y轴交于点C,顶点为D.
(2013•莆田)如图,抛物线y=ax2+bx+c的开口向下,与x轴交于点A(-3,0)和点B(1,0).与y轴交于点C,顶点为D.