题目内容
 (2013•莆田)如图,抛物线y=ax2+bx+c的开口向下,与x轴交于点A(-3,0)和点B(1,0).与y轴交于点C,顶点为D.
(2013•莆田)如图,抛物线y=ax2+bx+c的开口向下,与x轴交于点A(-3,0)和点B(1,0).与y轴交于点C,顶点为D.(1)求顶点D的坐标.(用含a的代数式表示);
(2)若△ACD的面积为3.
①求抛物线的解析式;
②将抛物线向右平移,使得平移后的抛物线与原抛物线交于点P,且∠PAB=∠DAC,求平移后抛物线的解析式.
分析:(1)已知抛物线与x轴的两交点的横坐标分别是-3和1,设抛物线解析式的交点式y=a(x+3)(x-1),再配方为顶点式,可确定顶点坐标;
(2)①设AC与抛物线对称轴的交点为E,先运用待定系数法求出直线AC的解析式,求出点E的坐标,即可得到DE的长,然后由S△ACD=
×DE×OA列出方程,解方程求出a的值,即可确定抛物线的解析式;
②先运用勾股定理的逆定理判断出在△ACD中∠ACD=90°,利用三角函数求出tan∠DAC=
.设y=-x2-2x+3=-(x+1)2+4向右平移后的抛物线解析式为y=-(x+m)2+4,两条抛物线交于点P,直线AP与y轴交于点F.根据正切函数的定义求出OF=1.分两种情况进行讨论:(Ⅰ)如图2①,F点的坐标为(0,1),(Ⅱ)如图2②,F点的坐标为(0,-1).针对这两种情况,都可以先求出点P的坐标,再得出m的值,进而求出平移后抛物线的解析式.
(2)①设AC与抛物线对称轴的交点为E,先运用待定系数法求出直线AC的解析式,求出点E的坐标,即可得到DE的长,然后由S△ACD=
| 1 |
| 2 |
②先运用勾股定理的逆定理判断出在△ACD中∠ACD=90°,利用三角函数求出tan∠DAC=
| 1 |
| 3 |
解答:解:(1)∵抛物线y=ax2+bx+c与x轴交于点A(-3,0)和点B(1,0),
∴抛物线解析式为y=a(x+3)(x-1)=ax2+2ax-3a,
∵y=a(x+3)(x-1)=a(x2+2x-3)=a(x+1)2-4a,
∴顶点D的坐标为(-1,-4a);
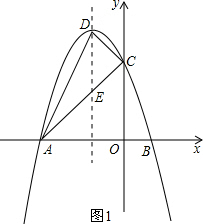 (2)如图1,①设AC与抛物线对称轴的交点为E.
(2)如图1,①设AC与抛物线对称轴的交点为E.
∵抛物线y=ax2+2ax-3a与y轴交于点C,
∴C点坐标为(0,-3a).
设直线AC的解析式为:y=kx+t,
则:
,
解得:
,
∴直线AC的解析式为:y=-ax-3a,
∴点E的坐标为:(-1,-2a),
∴DE=-4a-(-2a)=-2a,
∴S△ACD=S△CDE+S△ADE=
×DE×OA=
×(-2a)×3=-3a,
∴-3a=3,解得a=-1,
∴抛物线的解析式为y=-x2-2x+3;
②∵y=-x2-2x+3,
∴顶点D的坐标为(-1,4),C(0,3),
 ∵A(-3,0),
∵A(-3,0),
∴AD2=(-1+3)2+(4-0)2=20,CD2=(-1-0)2+(4-3)2=2,AC2=(0+3)2+(3-0)2=18,
∴AD2=CD2+AC2,
∴∠ACD=90°,
∴tan∠DAC=
=
=
,
∵∠PAB=∠DAC,
∴tan∠PAB=tan∠DAC=
.
如图2,设y=-x2-2x+3=-(x+1)2+4向右平移后的抛物线解析式为y=-(x+m)2+4,两条抛物线交于点P,直线AP与y轴交于点F.
∵tan∠PAB=
=
=
,
∴OF=1,则F点的坐标为(0,1)或(0,-1).
分两种情况:
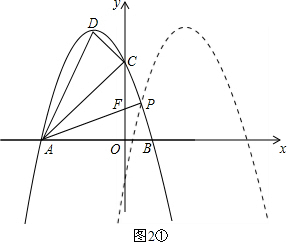
(Ⅰ)如图2①,当F点的坐标为(0,1)时,易求直线AF的解析式为y=
x+1,
由
,解得
,
(舍去),
∴P点坐标为(
,
),
将P点坐标(
,
)代入y=-(x+m)2+4,
得
=-(
+m)2+4,
解得m1=-
,m2=1(舍去),
∴平移后抛物线的解析式为y=-(x-
)2+4;
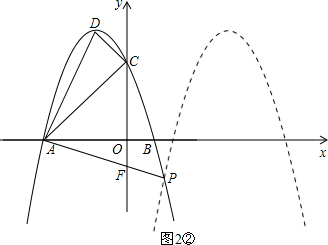 (Ⅱ)如图2②,当F点的坐标为(0,-1)时,易求直线AF的解析式为y=-
(Ⅱ)如图2②,当F点的坐标为(0,-1)时,易求直线AF的解析式为y=-
x-1,
由
,解得
,
(舍去),
∴P点坐标为(
,-
),
将P点坐标(
,-
)代入y=-(x+m)2+4,
得-
=-(
+m)2+4,
解得m1=-
,m2=1(舍去),
∴平移后抛物线的解析式为y=-(x-
)2+4;
综上可知,平移后抛物线的解析式为y=-(x-
)2+4或y=-(x-
)2+4.
∴抛物线解析式为y=a(x+3)(x-1)=ax2+2ax-3a,
∵y=a(x+3)(x-1)=a(x2+2x-3)=a(x+1)2-4a,
∴顶点D的坐标为(-1,-4a);
 (2)如图1,①设AC与抛物线对称轴的交点为E.
(2)如图1,①设AC与抛物线对称轴的交点为E.∵抛物线y=ax2+2ax-3a与y轴交于点C,
∴C点坐标为(0,-3a).
设直线AC的解析式为:y=kx+t,
则:
|
解得:
|
∴直线AC的解析式为:y=-ax-3a,
∴点E的坐标为:(-1,-2a),
∴DE=-4a-(-2a)=-2a,
∴S△ACD=S△CDE+S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
∴-3a=3,解得a=-1,
∴抛物线的解析式为y=-x2-2x+3;
②∵y=-x2-2x+3,
∴顶点D的坐标为(-1,4),C(0,3),
 ∵A(-3,0),
∵A(-3,0),∴AD2=(-1+3)2+(4-0)2=20,CD2=(-1-0)2+(4-3)2=2,AC2=(0+3)2+(3-0)2=18,
∴AD2=CD2+AC2,
∴∠ACD=90°,
∴tan∠DAC=
| CD |
| AC |
|
| 1 |
| 3 |
∵∠PAB=∠DAC,
∴tan∠PAB=tan∠DAC=
| 1 |
| 3 |
如图2,设y=-x2-2x+3=-(x+1)2+4向右平移后的抛物线解析式为y=-(x+m)2+4,两条抛物线交于点P,直线AP与y轴交于点F.
∵tan∠PAB=
| OF |
| OA |
| OF |
| 3 |
| 1 |
| 3 |
∴OF=1,则F点的坐标为(0,1)或(0,-1).
分两种情况:
(Ⅰ)如图2①,当F点的坐标为(0,1)时,易求直线AF的解析式为y=
| 1 |
| 3 |
由
|
|
|
∴P点坐标为(
| 2 |
| 3 |
| 11 |
| 9 |
将P点坐标(
| 2 |
| 3 |
| 11 |
| 9 |
得
| 11 |
| 9 |
| 2 |
| 3 |
解得m1=-
| 7 |
| 3 |
∴平移后抛物线的解析式为y=-(x-
| 7 |
| 3 |
 (Ⅱ)如图2②,当F点的坐标为(0,-1)时,易求直线AF的解析式为y=-
(Ⅱ)如图2②,当F点的坐标为(0,-1)时,易求直线AF的解析式为y=-| 1 |
| 3 |
由
|
|
|
∴P点坐标为(
| 4 |
| 3 |
| 13 |
| 9 |
将P点坐标(
| 4 |
| 3 |
| 13 |
| 9 |
得-
| 13 |
| 9 |
| 4 |
| 3 |
解得m1=-
| 11 |
| 3 |
∴平移后抛物线的解析式为y=-(x-
| 11 |
| 3 |
综上可知,平移后抛物线的解析式为y=-(x-
| 7 |
| 3 |
| 11 |
| 3 |
点评:此题是二次函数的综合题,考查了待定系数法求函数的解析式,二次函数的性质,勾股定理的逆定理,三角函数的定义,三角形的面积、两函数交点坐标的求法,函数平移的规律等知识,综合性较强,有一定难度,解题的关键是方程思想、数形结合思想与分类讨论思想的应用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 (2013•莆田)如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )
(2013•莆田)如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( ) (2013•莆田)如图,一次函数y=(m-2)x-1的图象经过二、三、四象限,则m的取值范围是( )
(2013•莆田)如图,一次函数y=(m-2)x-1的图象经过二、三、四象限,则m的取值范围是( )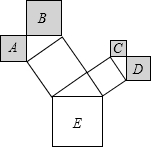 (2013•莆田)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为2,5,1,2.则最大的正方形E的面积是
(2013•莆田)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为2,5,1,2.则最大的正方形E的面积是