题目内容
【题目】如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( ) 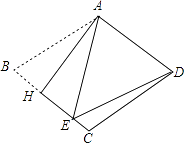
A.10°
B.15°
C.18°
D.20°
【答案】B
【解析】解:∵菱形ABCD沿AH折叠,B落在BC边上的点E处, ∴AB=AE,
∵∠BAE=40°,
∴∠B=∠AEB= ![]() (180°﹣40°)=70°,
(180°﹣40°)=70°,
在菱形ABCD中,AB=AD,∠ADC=∠B=70°,
AD∥BC,
∴∠DAE=∠AEB=70°,
∵AB=AE,AB=AD,
∴AE=AD,
∴∠ADE= ![]() (180°﹣∠DAE)=
(180°﹣∠DAE)= ![]() (180°﹣70°)=55°,
(180°﹣70°)=55°,
∴∠EDC=∠ADC﹣∠ADE=70°﹣55°=15°.
故选B.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
相关题目
【题目】某商场进行有奖促销活动.活动规则:购买500元商品就可以获得一次转转盘的机会(转盘被分为5个扇形区域,分别是特等奖、一等奖、二等奖、三等奖、纪念奖),转动转盘停止后,指针指在哪个获奖区域就可以获得该区域相应等级奖品一件(奖品设置如图所示).商场工作人员在制作转盘时,将获奖区域扇形圆心角分配如下表:
奖次 | 特等奖 | 一等奖 | 二等奖 | 三等奖 | 纪念奖 |
圆心角 | 1° | 10° | 30° | 90° | 229° |
(1)转动一次转盘,获得圆珠笔的概率是多少?
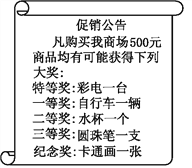
(2)如果不用转盘,请设计一种等效活动方案
(要求写清替代工具和活动规则).