题目内容
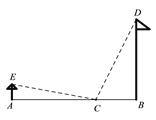
【题目】如图，小明所在学校的旗杆BD高约为13米，距离旗杆20米处刚好有一棵高约为3米的香樟树AE．活动课上，小明有意在旗杆与香樟树之间的连线上来回踱步，发现有一个位置到旗杆顶部与树顶的距离相等．请你求出该位置与旗杆之间的距离.
【答案】该位置与旗杆之间的距离为6米.
【解析】试题分析：
设这个点为点C，连接EC、DC，则由题意可知EC=DC，再设AC= 
米，则BC=（20- 
）米，在两个直角三角形中，由勾股定理分别表达出CE2和CD2，就可列出方程解得
的值，从而就可求出该位置与旗杆之间的距离.
试题解析：
根据题意可得：AE＝3m，AB＝20m，BD＝13m.
如图，设该位置为点C，且AC＝
m.
由AC＝
m得：BC＝(20－
)m.
由题意得：CE＝CD，则CE2＝CD2.
∴
，解得： 
＝14.
∴ CB＝20－
＝6.
由0＜14＜20可知，该位置是存在的.
答：该位置与旗杆之间的距离为6米.
练习册系列答案
相关题目
【题目】一方有难八方支援，某市政府筹集了抗旱必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）
车型 | 甲 | 乙 | 丙 |
汽车运载量（吨/辆） | 5 | 8 | 10 |
汽车运费（元/辆） | 400 | 500 | 600 |
（1）若全部物资都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？
（2）为了节约运费，该市政府可以调用甲、乙、丙三种车型参与运送，已知它们的总辆数为16辆，你能通过列方程组的方法分别求出几种车型的辆数吗？
（3）求出那种方案的运费最省？最省是多少元．
