题目内容
【题目】在△ABC中，∠A=36°，AB=AC，BD是△ABC的角平分线，下列结论：
①△ABD，△BCD都是等腰三角形；
②AD=BD=BC；
③BC2=CDCA；
④D是AC的黄金分割点
其中正确的是（ ）
A．1个 B．2个 C．3个 D．4个
【答案】D
【解析】
试题分析：在△ABC，AB=AC，∠A=36°，BD平分∠ABC交AC于点D，可推出△BCD，△ABD为等腰三角形，可得AD=BD=BC，利用三角形相似解题．
解：如图，∵AB=AC，∠A=36°，
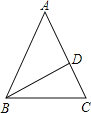
∴∠ABC=∠C=72°，
∵BD平分∠ABC交AC于点D，
∴∠ABD=∠CBD=
∠ABC=36°=∠A，
∴AD=BD，
∠BDC=∠ABD+∠A=72°=∠C，
∴BC=BD，
∴△ABD，△BCD都是等腰三角形，故①正确；
∴BC=BD=AD，故②正确；
∵∠A=∠CBD，∠C=∠C，
∴△BCD∽△ACB，
∴
，
即BC2=CDAC，故③正确；
∵AD=BD=BC，
∴AD2=ACCD=（AD+CD）CD，
∴AD=
CD，
∴D是AC的黄金分割点．故④正确，
故选D．
练习册系列答案
相关题目
