题目内容
 已知点P(x,y)是第一象限内的一个动点,且满足x+y=4.请先在所给的平面直角坐标系中画出函数y=2x+1的图象,该图象与x轴交于点A,然后解答下列问题:
已知点P(x,y)是第一象限内的一个动点,且满足x+y=4.请先在所给的平面直角坐标系中画出函数y=2x+1的图象,该图象与x轴交于点A,然后解答下列问题:(1)利用所画图象,求当-1≤y≤3时x的取值范围;
(2)若点P正好也在直线y=2x+1上,求点P的坐标;
(3)设△OPA的面积为S,求S关于点P的横坐标x的函数解析式.
分析:(1)因为函数为一次函数,所以当y=-1时x=-1,当y=3时,x=1,即得出x的范围;(2)点P正好也在直线y=2x+1上,又点P也在直线x+y=4上,所以联立方程可解出P的坐标;(3)本问即求x与S的关系式,用x表达出△OPA的面积即可.
解答: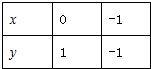 解:列表,连线画图
解:列表,连线画图
(1)由图象可得,当y=-1时x=-1,当y=3时x=1
∴x的取值范围为-1≤x≤1,
(2)点P正好也在直线y=2x+1上,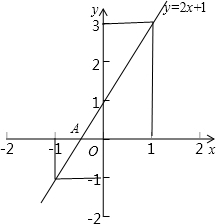
可得:
,
解得
,所以点P的坐标为(1,3);
(3)依题意得:对于y=2x+1,令当y=0得x=-
点A坐标为(-
,0)
∵点P(x,y)是第一象限内,且x+y=4.
∴x的取值范围为0<x<4
△OPA的面积S=
×|-
|×|4-x|=
=
,
即S关于点P的横坐标x的函数解析式为S=
.
 解:列表,连线画图
解:列表,连线画图(1)由图象可得,当y=-1时x=-1,当y=3时x=1
∴x的取值范围为-1≤x≤1,
(2)点P正好也在直线y=2x+1上,

可得:
|
解得
|
(3)依题意得:对于y=2x+1,令当y=0得x=-
| 1 |
| 2 |
| 1 |
| 2 |
∵点P(x,y)是第一象限内,且x+y=4.
∴x的取值范围为0<x<4
△OPA的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| |4-x| |
| 4 |
| 4-x |
| 4 |
即S关于点P的横坐标x的函数解析式为S=
| 4-x |
| 4 |
点评:本题考查了一次函数的知识,难度适中,关键是掌握正确画出函数图象.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知点A(a,
)是两函数y=kx-2与y=(
-1)x图象的交点.则实数k等于( )
| 2 |
| 2 |
A、-
| ||
B、1-
| ||
C、
| ||
| D、1 |