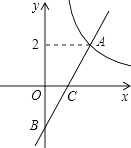题目内容
【题目】若a、b满足,![]() 且A(a,0)、B(0,b)
且A(a,0)、B(0,b)

(1) 如图,在x正半轴上有一点C(x,0).若△ABC的面积大于6,请直接写出x的取值范围____________;
(2)若在平面直角坐标系第四象限上存在一点N,N的坐标为(n,﹣n),满足4≤S△ABN≤8,求n的取值范围.
(3)若在平面直角坐标系上存在一点M,M的坐标为(m,﹣2m),请通过计算说明:无论m取何值△ABM的面积为定值,并求出这个值.
【答案】(1)![]() ;(2)
;(2) ![]() (3) 无论m取何值△ABM的面积为定值,面积为1个单位平方,证明见解析.
(3) 无论m取何值△ABM的面积为定值,面积为1个单位平方,证明见解析.
【解析】
(1)根据非负数的性质求出a,b的值,得到A,B点的坐标,根据三角形面积公式列出不等式求解即可;
(2)分N点在直线AB左侧时(n>0)和右侧时(n>0)两种情况求解,分别求出S△ABN用n表示的代数式,再解不等式组即可;
(3)分三种情况,根据三角形面积计算公式进行求解即可.
(1) ∵![]()
∴![]()
解得,![]()
∴A(1,0),B(0,2)
∴OA=1,OB=2,
∵C(x,0)
∴AC=x-1
∴S△ABC=![]()
解得,![]() ,
,
故答案为:![]() ;
;
(2)当N点在直线AB左侧时(n>0)
过N做NF⊥x轴于F,做NE⊥y轴于E,
∵N(n,﹣n),A(1,0),B(0,2),
∴AO=1,BO=2,EN=FN=n
∴S△ABN=S△AON+S△ABO﹣S△OBN
∴S△ABN=![]()
∴![]() ∴
∴![]() ,不合题意舍去;
,不合题意舍去;
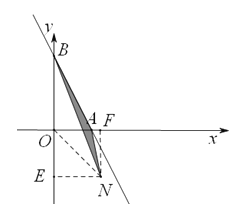
当N点在直线AB右侧时(n>0)
过N做NF⊥x轴于F,做NE⊥y轴于E,
∵N(n,﹣n),A(1,0),B(0,2),
∴AO=1,BO=2,EN=FN=n
∴S△ABN=S△BON﹣S△ABO﹣S△AON
∴S△ABN=![]()
∴![]() ∴
∴![]()
综上所述:n的取值范围为![]()

(3)证明:1)当点M为原点(m=0)时, S△ABM=1
2)当点M(m<0)在第二象限时,如图:
过M做ME⊥x轴于E,做MF⊥y轴于F
∵M(m,﹣2m),A(1,0),B(0,2),
∴MF=﹣m,EM=﹣2m,AO=1,BO=2,
∴S△ABM=S△BOM+S△ABO﹣S△OAM
∴S△ABM=![]()
∴S△ABM=1
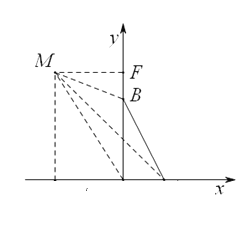
3)当点M(m>0)在第四象限时,如图:
过M做EF⊥x轴于F,过B点做BE⊥EF于E
∵M(m,﹣2m),A(1,0),B(0,2),
∴MF=m,EM=2m,AO=1,BO=2,
∴S△ABM=S△AOM+S△ABO﹣S△BOM
∴S△ABM=![]()
∴S△ABM=1
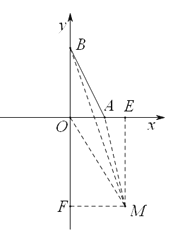
综上所述:无论m取何值△ABM的面积为定值,面积为1个单位平方.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案