题目内容
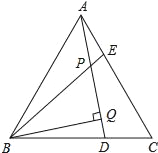
【题目】已知:如图,△ABC中,AD⊥BC,AB=AE,点E在AC的垂直平分线上.
(1)请问:AB、BD、DC有何数量关系;并说明理由.
(2)如果∠B=60°,证明:CD=3BD.

【答案】(1)AB+BD=CD;理由见解析;(2)证明见解析.
【解析】
(1)由AD⊥BC,BD=DE,点E在AC的垂直平分线上,根据线段垂直平分线的性质,可得AE=EC,AB=AE,继而证得AB+BD=AE+DE=DC.
(2)易得△ABE是等边三角形,则可得△ABC是直角三角形,且∠BAD=∠C=30°,然后由含30°角的直角三角形的性质,证得结论.
解:(1)AB+BD=DC.理由如下:
∵AD⊥BC,BD=DE,∴AB=AE,BD=DE,
∵点E在AC的垂直平分线上,∴AE=CE,
∴AB+BD=AE+DE=DC.
(2)∵AB=AE,∠B=60°,∴△ABE是等边三角形,∴∠AEB=∠B=∠BAE=60°,
∵AE=EC,∴∠C=∠CAE=![]() ∠AEB=30°,∴∠BAC=90°,∠BAD=30°,
∠AEB=30°,∴∠BAC=90°,∠BAD=30°,
在Rt△ABC中,BC=2AB,在Rt△AABD中,AB=2BD,
∴BC=4BD,
∴DC=3BD.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目