Question

【题目】（1）如图1，AB∥CD，点P在AB、CD外部，若∠B=60°，∠D=30°，则∠BPD= °；

（2）如图2，AB∥CD，点P在AB、CD内部，则∠B，∠BPD，∠D之间有何数量关系？证明你的结论；

（3）在图2中，将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M，如图3，若∠BPD=86°，∠BMD=40°，求∠B＋∠D的度数．

图1 图2 图3

Answer 1

【答案】（1）30°；（2）∠BPD＝∠B+∠D，证明见解析；（3）46°．

【解析】

（1）根据平行线的性质可求得∠BOD的度数，由三角形外角的性质即可求得结果；

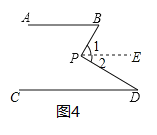
（2）过点P作PE∥AB，如图4，由平行公理的推论可得AB∥PE∥CD，然后根据平行线的性质和角的和差即可得出结论；

（3）延长BP交CD于点E，如图5，根据三角形外角的性质可得∠BPD＝∠BMD+∠B+∠D，进一步即可求出结果．

解：（1）∵AB∥CD，∠B＝60°，

∴∠BOD＝∠B＝60°，

∴∠BPD＝∠BOD﹣∠D＝60°﹣30°＝30°．

故答案为：30°；

（2）∠BPD＝∠B+∠D．

证明：过点P作PE∥AB，如图4，

∵AB∥CD，

∴AB∥PE∥CD，

∴∠1＝∠B，∠2＝∠D，

∴∠BPD＝∠1+∠2＝∠B+∠D；

（3）延长BP交CD于点E，如图5，

∵∠1＝∠BMD+∠B，∠BPD＝∠1+∠D，

∴∠BPD＝∠BMD+∠B+∠D，

∵∠BPD＝86°，∠BMD＝40°，

∴∠B+∠D＝∠BPD﹣∠BMD＝86°﹣40°＝46°．