题目内容
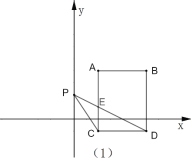
【题目】已知点A(1,2)、点 B在双曲线y= ![]() (x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,
(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,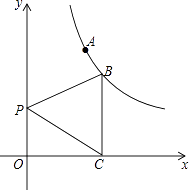
(1)求k的值及△PBC的面积;
(2)设点M(x1 , y1)、N(x2 , y2)(x2>x1>0)是双曲线y= ![]() (x>0)上的任意两点,s=
(x>0)上的任意两点,s= ![]() ,t=
,t= ![]() ,试判断s与t的大小关系,并说明理由.
,试判断s与t的大小关系,并说明理由.
【答案】
(1)解:把A(1,2)代入y= ![]() 得k=2;
得k=2;
设B的坐标是(m,n)则mn=2,BC=n,OC=m.
则S△PBC= ![]() BCOC=
BCOC= ![]() mn=1
mn=1
(2)解:s>t;
理由:∵s﹣t= ![]()
═ ![]()
═ ![]() =
= ![]() ,
,
∵x2>x1>0,
∴ ![]() >0,x1x2(x1+x2)>0,
>0,x1x2(x1+x2)>0,
∴ ![]() ;
;
∴s>t
【解析】(1)利用待定系数法即可求得k的值;设B的坐标是(m,n)则mn=2,BC=n,OC=m,利用三角形的面积公式求解;(2)把y1和y2用x1和x2,然后求s﹣t得值,对式子进行变形判断s﹣t的符号即可。
【考点精析】解答此题的关键在于理解比例系数k的几何意义的相关知识,掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】为了激发学生爱数学、学数学、用数学的热情,某学校在七年级开展“魅力数学”趣味竞赛,该校七年级共有学生400人参加竞赛.现随机抽取40名参赛学生的成绩数据(百分制)进行整理、描述和分析.
74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
范围 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
频数 | 1 | m | 13 | 9 | 14 |
平均数、中位数、众数如下表所示:
平均数 | 中位数 | 众数 |
84.1 | n | 89 |
根据以上信息,回答下列问题:
(1)m= ,n= ;
(2)小明说:“这次竞赛我得了84分,在所有参赛学生中排名属中等偏上!”小明的说法 (填“正确”或“不正确”),理由是 ;
(3)若成绩不低于85分可以进入决赛,估计参赛的400名学生中能进入决赛的人数.
【题目】某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图,趣题巧解,数学应用,魔方复原,每个项目得分都按一定百分比折算后记入总分,下表为甲,乙,丙三位同学得分情况(单位:分)
七巧板拼图 | 趣题巧解 | 数学应用 | 魔方复原 | |
甲 | 66 | 89 | 86 | 68 |
乙 | 66 | 60 | 80 | 68 |
丙 | 66 | 80 | 90 | 68 |
(1)比赛后,甲猜测七巧板拼图,趣题巧解,数学应用,魔方复原这四个项目得分分别按10%,40%,20%,30%折算△记入总分,根据猜测,求出甲的总分;
(2)本次大赛组委会最后决定,总分为80分以上(包含80分)的学生获一等奖,现获悉乙,丙的总分分别是70分,80分.甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分,问甲能否获得这次比赛的一等奖?