题目内容
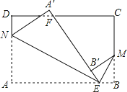
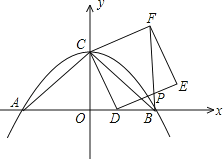
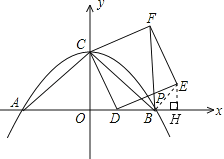
【题目】如图,抛物线y=﹣![]() x2+4交x轴于点A、B,交y轴于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF,交DE于点P.
x2+4交x轴于点A、B,交y轴于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF,交DE于点P.
(1)试判断△ABC的形状,并说明理由;
(2)求证:BF⊥AB.
(3)当点D从点O沿x轴正方向移动到点B时,点E所走过的路线长为______;
(4)探究当点D在何处时,△FBC是等腰三角形,并求出相应的BF的长.
【答案】(1)△ABC是等腰直角三角形;理由见解析;(2)证明见解析;(3)![]() ;(4)AD=CD时,BF=4;AC=AD时,BF=4
;(4)AD=CD时,BF=4;AC=AD时,BF=4![]() ;AC=BC时,BF=8.
;AC=BC时,BF=8.
【解析】
(1)根据二次函数与坐标轴的交点的求法求出A、B、C,再求出OA、OB、OC,然后根据等腰直角三角形的判定解答;
(2)根据等腰直角三角形的性质和正方形的性质,求出AC=BC,CD=CF,∠ACD=∠BCF,然后利用“边角边”证明△ACD和△BCF全等,根据全等三角形对应角相等可得∠CBF=∠CAD=45°,然后求出∠ABF=90°,再根据垂直的定义证明即可;
(3)过点E作EH⊥x轴于H,连接BE,求出∠OCD=∠HDE,然后利用“角角边”证明△OCD和△HDE全等,根据全等三角形对应边相等可得EH=OD,OC=DH,然后求出△BEH是等腰直角三角形,根据等腰直角三角形的性质表示出BE,从而判断出点E走过的路线长为BC的长度,然后求解即可;
(4)根据全等三角形对应边相等可得AD=BF,利用勾股定理列式求出AC,然后分AD=CD,AC=AD,AC=BC三种情况讨论求解得到AD,即为FB的长.
(1)解:令x=0,得y=4,
∴C(0,4),
令y=0,则﹣![]() x2+4=0,
x2+4=0,
解得:x1=4,x2=﹣4,
∴A(﹣4,0),B(4,0),
∴OA=OB=OC=4,
∴△ABC是等腰直角三角形;
(2)证明:如图,
∵△ABC是等腰直角三角形,CDEF是正方形,
∴AC=BC,CD=CF,∠ACD=∠BCF,
在△ACD和△BCF中,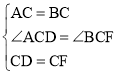 ,
,
∴△ACD≌△BCF(SAS),
∴∠CBF=∠CAD=45°,
∴∠ABF=∠ABC+∠CBF=90°,
∴BF⊥AB;
(3)如图,过点E作EH⊥x轴于H,连接BE,

∵∠OCD+∠ODC=∠HDE+∠ODC=90°,
∴∠OCD=∠HDE,
在△OCD和△HDE中,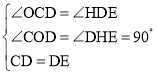 ,
,
∴△OCD≌△HDE(AAS),
∴EH=OD,OC=DH,
∵OD+BD=OB=OC,
BH+BD=DH,
∴OD=BH=EH,
∴△BEH是等腰直角三角形,
∴BE=![]() EH,
EH,
∵点D从点O沿x轴正方向移动到点B,
∴点E所走过的路线长为为BC的长度,是4![]() ;
;
故答案为:4![]() .
.
(4)∵△ACD≌△BCF,
∴AD=BF,
由勾股定理得,AC=![]() =
=![]() =4
=4![]() ,
,
①若AD=CD,则点O、D重合,BF=AO=4,
②若AC=AD,则BF=AD=4![]() ,
,
③若AC=BC,则BF=AD=AB=8,
综上所述,BF=4或4![]() 或8.
或8.