题目内容
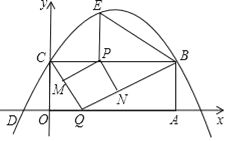
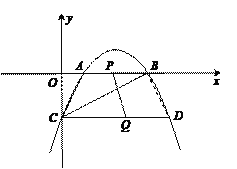
【题目】如图,抛物线y=-![]() x2+
x2+![]() x-2与x轴相交于点A、B,与y轴相交于点C.
x-2与x轴相交于点A、B,与y轴相交于点C.
(1)求证:△AOC∽△COB;
(2)过点C作CD∥x轴交抛物线于点D.若点P在线段AB上以每秒1个单位的速度由A向B运动,同时点Q在线段CD上也以每秒1个单位的速度由D向C运动,则经过几秒后,PQ=AC.

【答案】(1)证明见解析;(2)经过2.5秒或 1.5秒时,PQ=AC.
【解析】试题分析:(1)可先根据抛物线的解析式求出A,B,C的坐标,然后看OA,OC,OB是否对应成比例即可;
(2)根据抛物线的对称性可知:AC=BD,四边形ABDC为等腰梯形,那么本题可分两种情况进行求解:
①当四边形APQC是等腰梯形,即四边形PQDB是平行四边形时,AC=PQ,那么QD=PB,可据此来求t的值.
②当四边形ACQP是平行四边形时,AC=PQ,那么此时AP=CQ,可据此求出t的值.
试题解析:(1)解:(1)当y=0时,即![]() =0,得x1=1,x2=4 .当x=0时,y=-2.
=0,得x1=1,x2=4 .当x=0时,y=-2.
∴ A(1,0),B(4,0),C(0,-2).
∴OA=1,OB=4,OC=2 ,
∴![]() ,
, ![]()
![]() .
.
又∵∠AOC=∠BOC ∴△AOC∽△COB.
(2)设经过t秒后,PQ=AC.由题意得:AP=DQ= t
∵A(1,0)、B(4,0) ∴AB=3 , ∴BP=3-t ‘
∵CD∥x轴,点C(0,-2) ∴点D的纵坐标为-2.
∵点D在抛物线y=![]() 上
上
∴D(5,-2) ∴CD=5 ∴CQ=5-t
① 当AP=CQ,即四边形APQC是平行四边形时, PQ=AC.
t=5-t ∴t=2.5.
② 连结BD,当DQ=BP,即四边形PBDQ是平行四边形时,
PQ=BD=AC.
t=3-t ∴t=1.5.
所以,经过2.5秒或 1.5秒时,PQ=AC.

【题目】常常听说“勾3股4弦5”,是什么意思呢?它就是勾股定理,即“直角三角形两直角边长a,b与斜边长c之间满足等式:a2+b2=c2”的一个最简单特例.我们把满足a2+b2=c2的三个正整数a,b,c,称为勾股数组,记为(a,b,c).
(1)请在下面的勾股数组表中写出m、n、p合适的数值:
a | b | c | a | b | c |
3 | 4 | 5 | 4 | 3 | 5 |
5 | 12 | m | 6 | 8 | 10 |
7 | 24 | 25 | p | 15 | 17 |
9 | n | 41 | 10 | 24 | 26 |
11 | 60 | 61 | 12 | 35 | 37 |
… | … | … | … | … | … |
平面直角坐标系中,横、纵坐标均为整数的点叫做整点(格点).过x轴上的整点作y轴的平行线,过y轴上的整点作x轴的平行线,组成的图形叫做正方形网格(有时简称网格),这些平行线叫做格边,当一条线段AB的两端点是格边上的点时,称为AB在格边上.顶点均在格点上的多边形叫做格点多边形.在正方形网格中,我们可以利用勾股定理研究关于图形面积、周长的问题,其中利用割补法、作图法求面积非常有趣.
(2)已知△ABC三边长度为4、13、15,请在下面的网格中画出格点△ABC并计算其面积.