题目内容
【题目】如图,双曲线y=![]() (x>0)的图象经过点A(
(x>0)的图象经过点A(![]() ,4),直线y=
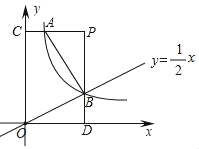
,4),直线y=![]() x与双曲线交于B点,过A,B分别作y轴、x轴的垂线,两线交于P点,垂足分别为C,D.
x与双曲线交于B点,过A,B分别作y轴、x轴的垂线,两线交于P点,垂足分别为C,D.
(1)求双曲线的解析式;
(2)求证:△ABP∽△BOD.
【答案】(1)![]() ;(2)详见解析;
;(2)详见解析;
【解析】
(1)将点A坐标代入反比例函数解析式中,即可得出结论;
(2)先求出点B坐标,进而求出OD,BD,进而判断出![]() ,即可得出结论.
,即可得出结论.
(1)∵点A(![]() ,4)在双曲线y=
,4)在双曲线y=![]() 上,
上,
∴k=![]() ×4=2,
×4=2,
∴双曲线的解析式为y=![]() ;
;
(2)如图,
由(1)知,双曲线的解析式为y=![]() ①,
①,
直线OB的解析式为y=![]() x②,
x②,
连接①②解得,![]() 或
或![]() (舍去),
(舍去),
∴B(2,1),
∴BD=1,OD=2,
∵CP⊥y轴,PD⊥x轴,
∴∠OCP=∠ODP=90°=∠COD,
∴四边形OCPD是矩形,
∴∠ODB=∠P=90°,
CP=OD=2,PD=OC,
∵A(![]() ,4),
,4),
∴OC=4,CA=![]() ,
,
∴AP=CP﹣AC=![]() ,BP=PD﹣1=3,
,BP=PD﹣1=3,
∴![]() ,
,
∴![]() ,
,
∵∠P=∠ODB=90°,
∴△ABP∽△BOD.

练习册系列答案
相关题目