题目内容
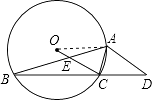
【题目】如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点. 
(1)求∠D的度数;
(2)求证:AC2=ADCE.
【答案】
(1)解:连接OA,如图所示:
∵圆周角∠ABC与圆心角∠AOC所对的弧都为 ![]() ,
,
∴∠AOC=2∠ABC,又∠ABC=15°,
∴∠AOC=30°,
又OA=OC,∴∠OAC=∠OCA= ![]() =75°,
=75°,
又∠BAC=45°,∠ABC=15°,
∴∠ACB=120°,
∴∠OCB=∠ACB﹣∠ACO=120°﹣75°=45°,
又OC∥AD,
∴∠D=∠OCB=45°
(2)证明:∵∠ABC=15°,∠OCB=45°,
∴∠AEC=60°,
又∠ACB=120°∴∠ACD=60°,
∴∠AEC=∠ACD=60°,
∵∠D=45°,∠ACD=60°,
∴∠CAD=75°,又∠OCA=75°,
∴∠CAD=∠OCA=75°,
∴△ACE∽△DAC,
∴ ![]() =
= ![]() ,即AC2=ADCE
,即AC2=ADCE
【解析】(1)连接OA,由圆周角∠ABC与圆心角∠AOC所对的弧为同一条弧,根据同弧所对的圆心角等于所对圆周角的2倍,由∠ABC的度数求出∠AOC的度数,再由OA=OC,根据等边对等角,由顶角∠AOC的度数,利用三角形的内角和定理求出底角∠ACO的度数,再由∠BAC及∠ABC的度数,求出∠ACB的度数,由∠ACB﹣∠ACO求出∠BCE的度数,由OC与AD平行,根据两直线平行同位角相等可得∠D=∠BCE,可得出∠D的度数;(2)由∠ACB的度数,利用邻补角定义求出∠ACD的度数,再由∠AEC为三角形BEC的外角,利用外角性质得到∠AEC=∠ABC+∠BCE,可得出∠AEC的度数,进而得到∠AEC=∠ACD,在三角形ACD中,由∠ACD及∠D的度数,求出∠CAD的度数,可得∠CAD=∠ACE,利用两对对应角相等的三角形相似可得三角形AEC与三角形DCA相似,根据相似三角形的对应边成比例可得证.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.