题目内容
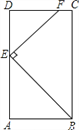
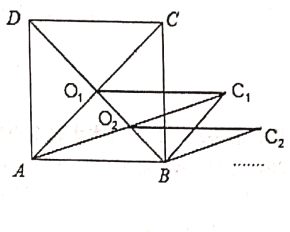
【题目】如图所示，矩形ABCD的面积为10cm2，它的两条对角线交于点O1，以AB、AO1为邻边作平行四边形ABC1O1，平行四边形ABC1O1的对角线交于点O2；同样以AB、AO2为邻边作平行四边形ABC2O2，……依此类推，则平行四边形ABC5O5的面积为( )
A.
B.
C.
D.
【答案】D
【解析】
根据矩形对角线互相平分的性质可知O是AC与DB的中点，则平行四边形的ABC1O1的高为矩形的高的一半，底和矩形边长相等，则平行四边形的ABC1O1的面积=
S矩形ABCD，ABC２O２的面积=平行四边形的ABC1O1的面积，即，ABC２O２的面积=
S矩形ABCD，依次类推ABC5O5的面积为
S矩形ABCD，即可确定答案.
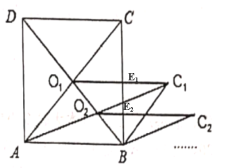
解：如图，O1C1，O2C2分别交BC于E1，E2
∵矩形ABCD，
∴AO1=AC
∵平行四边形ABC1O1
∴C1O1∥AB
∴BE1=BC
又∵矩形的长和平行四边形的底相等，高为BE1
∴平行四边形ABC1O1=S矩形ABCD
同理: 平行四边形ABC2O2的面积是平行四边形的ABC1O1的面积的一半
∴平行四边形ABC２O２的面积=S矩形ABCD
以此类推，可得ABC5O5的面积为S矩形ABCD=×10=
故选：D.
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
