题目内容
 如图,三个等圆⊙O,⊙M,⊙N的圆心均在x轴上,其中⊙O分别与⊙N、⊙M外切,且⊙M,⊙N分别经过点A(-45,0),B(45,0).点G是⊙N上的一个动点,线段AG与y轴、⊙O分别交于点H、E、F,已知点K的坐标是(0,45).当△AKH的面积最小时,则⊙O的弦EF长为
如图,三个等圆⊙O,⊙M,⊙N的圆心均在x轴上,其中⊙O分别与⊙N、⊙M外切,且⊙M,⊙N分别经过点A(-45,0),B(45,0).点G是⊙N上的一个动点,线段AG与y轴、⊙O分别交于点H、E、F,已知点K的坐标是(0,45).当△AKH的面积最小时,则⊙O的弦EF长为24
24
.分析:要使△AKH的面积最小,边KH上的高AO的值是45,只要KH最小即可,过A作AG切⊙N于G,此时KH最小,连接NG,OE,过O作OC⊥EF于C,求出AO、AN,证△ACO∽△AGN,得出比例式,求出OC,在△EOC中根据勾股定理求出EC,根据垂径定理得出EF=2CE,代入求出即可.
解答:解: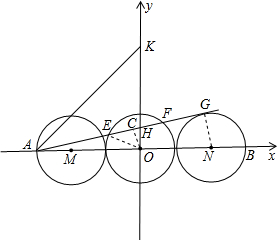 ∵要使△AKH的面积最小,边KH上的高AO的值是45,只要KH最小即可;
∵要使△AKH的面积最小,边KH上的高AO的值是45,只要KH最小即可;
∴过A作AG切⊙N于G,此时KH最小,
连接NG,OE,过O作OC⊥EF于C,
则∠OCA=∠NGA=90°,
∵A(-45,0),B(45,0),三个等圆⊙O、⊙M、⊙N,
∴三个圆的半径是(45+45)÷3÷2=15,
即GN=15,AO=45,AN=90-15=75,
∵∠OCA=∠NGA=90°,
∠GAN=∠GAN,
∴△ACO∽△AGN,
∴
=
,
∴
=
,
∴OC=9,
在Rt△EOC中,由勾股定理得:EC=
=
=12,
∵OC⊥EF,OC过圆心O,
∴由垂径定理得:EF=2CE=24.
故答案为:24.
 ∵要使△AKH的面积最小,边KH上的高AO的值是45,只要KH最小即可;
∵要使△AKH的面积最小,边KH上的高AO的值是45,只要KH最小即可;∴过A作AG切⊙N于G,此时KH最小,
连接NG,OE,过O作OC⊥EF于C,
则∠OCA=∠NGA=90°,
∵A(-45,0),B(45,0),三个等圆⊙O、⊙M、⊙N,
∴三个圆的半径是(45+45)÷3÷2=15,
即GN=15,AO=45,AN=90-15=75,
∵∠OCA=∠NGA=90°,
∠GAN=∠GAN,
∴△ACO∽△AGN,
∴
| AO |
| AN |
| OC |
| GN |
∴
| 45 |
| 75 |
| OC |
| 15 |
∴OC=9,
在Rt△EOC中,由勾股定理得:EC=
| OE2-OC2 |
| 152-92 |
∵OC⊥EF,OC过圆心O,
∴由垂径定理得:EF=2CE=24.
故答案为:24.
点评:本题考查了勾股定理,切线的性质,相似三角形的性质和判定,坐标与图形性质,垂径定理,三角形的面积等知识点,解此题的突破口是找出符合条件的G的位置,题目比较好,综合性比较强,有一定的难度.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
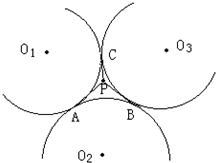 如图,三个等圆两两外切于点A﹑B﹑C,在圆弧AB﹑BC﹑CA所围成的曲线区域内任取一点P,边接PA﹑PB﹑PC,试问:以PA﹑PB﹑PC为边长能否组成一个锐角三角形?证明你的结论.
如图,三个等圆两两外切于点A﹑B﹑C,在圆弧AB﹑BC﹑CA所围成的曲线区域内任取一点P,边接PA﹑PB﹑PC,试问:以PA﹑PB﹑PC为边长能否组成一个锐角三角形?证明你的结论. 如图,三个等圆两两外切于点A﹑B﹑C,在圆弧AB﹑BC﹑CA所围成的曲线区域内任取一点P,边接PA﹑PB﹑PC,试问:以PA﹑PB﹑PC为边长能否组成一个锐角三角形?证明你的结论.
如图,三个等圆两两外切于点A﹑B﹑C,在圆弧AB﹑BC﹑CA所围成的曲线区域内任取一点P,边接PA﹑PB﹑PC,试问:以PA﹑PB﹑PC为边长能否组成一个锐角三角形?证明你的结论.