题目内容
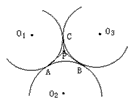
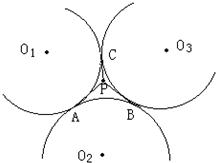如图，三个等圆两两外切于点A﹑B﹑C，在圆弧AB﹑BC﹑CA所围成的曲线区域内任取一点P，边接PA﹑PB﹑PC，试问：以PA﹑PB﹑PC为边长能否组成一个锐角三角形？证明你的结论．分析：因为三个等圆两两外切，根据相切两圆的性质可得：PA、PB、PC的边长组成的三角形，又P在正三角形ABC的内部，再由等边三角形的判断定理和性质即可逐步证明．
解答：
证明：以PA﹑PB﹑PC为边长能组成一个锐角三角形，
证明如下：
连接O1O2、O1O3、O2O3，AB、BC、AC，易证△O1O2O3，△ABC都是正三角形
把△APB绕点A旋转60°至△ACPˊ，得△APPˊ是正三角形
PˊC=PB，PA=PPˊ
∴△PP′C就是以PA、PB、PC的边长组成的三角形
记∠APB=α，∠BPC=β，∠APC=γ
∵P在正三角形ABC的内部
∴α＞60°，β＞60°，γ＞60°
又∵P在弧AB的外部，弧AB所含的圆周角为150°
∴α＜150°，同理β＜150°，γ＜150°
∵∠PPˊC=∠APˊC-60°=α-60°，∠CPPˊ=∠CPA-60°=γ-60°
∴∠PˊCP=180°-（α-60°）-（γ-60°）=300°-（α+γ）=β-60°，
∵60°＜α，β，γ＜150°
∴0°＜α-60°，β-60°，γ-60°＜90°
∴△PP′C为锐角三角形．
证明：以PA﹑PB﹑PC为边长能组成一个锐角三角形，证明如下：
连接O1O2、O1O3、O2O3，AB、BC、AC，易证△O1O2O3，△ABC都是正三角形
把△APB绕点A旋转60°至△ACPˊ，得△APPˊ是正三角形
PˊC=PB，PA=PPˊ
∴△PP′C就是以PA、PB、PC的边长组成的三角形
记∠APB=α，∠BPC=β，∠APC=γ
∵P在正三角形ABC的内部
∴α＞60°，β＞60°，γ＞60°
又∵P在弧AB的外部，弧AB所含的圆周角为150°
∴α＜150°，同理β＜150°，γ＜150°
∵∠PPˊC=∠APˊC-60°=α-60°，∠CPPˊ=∠CPA-60°=γ-60°
∴∠PˊCP=180°-（α-60°）-（γ-60°）=300°-（α+γ）=β-60°，
∵60°＜α，β，γ＜150°
∴0°＜α-60°，β-60°，γ-60°＜90°
∴△PP′C为锐角三角形．
点评：本题主要考查了线切两圆的性质及等边三角形的判断定理和性质，难度较大，关键是在做题前画出正确的辅助线．
练习册系列答案
相关题目
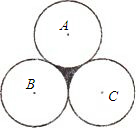如图，三个半径为1的等圆两两相外切，则中间围成的阴影部分面积为
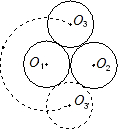如图，三个半径为1的等圆两两外切，若固定⊙O1和⊙O2，将⊙O3沿⊙O1的边缘逆时针旋转到⊙O3′的位置（即⊙O1、⊙O2、⊙O3′两两外切），圆心O3所经过的路程为（ ）
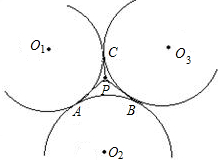如图，三个等圆两两外切于点A﹑B﹑C，在圆弧AB﹑BC﹑CA所围成的曲线区域内任取一点P，边接PA﹑PB﹑PC，试问：以PA﹑PB﹑PC为边长能否组成一个锐角三角形？证明你的结论．