Question

【题目】如图，在四边形ABCD中，AD∥BC, AB=AC，BE=CE=AD.

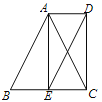
（1）求证：四边形ECDA是矩形；

（2）当△ABC是什么类型的三角形时，四边形ECDA是正方形？请说明理由.

Answer 1

【答案】(1)、证明过程见解析；(2)、当△ABC是等腰直角三角形时；证明过程见解析.

【解析】

试题分析：(1)、根据AD//EC且AD=EC得到平行四边形，然后根据AB=AC，BE=CE得出∠AEC=90°，则得到矩形；(2)、根据等腰直角三角形的性质得出AE=EC，从而得到正方形.

试题解析：(1)、在四边形AECD中,AD//EC且AD=EC. ∴ 四边形AECD是平行四边形

∵AB=AC，BE=CE ∴AE⊥BC ,∠AEC=90° ∴四边形AECD是矩形

、当△ABC是等腰直角三角形时，四边形ECDA是正方形

∵△ABC等腰直角三角形时，∠AEC=Rt∠,又因BE=CE ∴AE = =CE

又∵四边形AECD是矩形 ∴四边形ECDA是正方形