Question

【题目】如图1，长方形ABCD中，∠A=∠B=∠C=∠D=90°，AB=CD，AD=BC，且+|BC﹣6|=0，点P、Q分别是边AD、AB上的动点．

（1）求BD的长（长度单位是cm）；

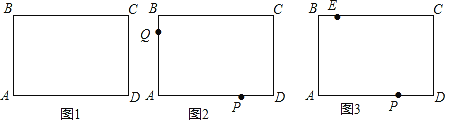
（2）如图2，若点P从D点出发，以2cm/s的速度沿DA向点A运动，点Q从B点出发，以1cm/s的速度沿BA向点A运动，P、Q同时出发，一个点到达终点时，两点同时停止运动；设运动时间为x，用含x的代数式表示△CPQ的面积S．

（3）如图3，在BC上取一点E，使EB=1，那么当△EPC是等腰三角形时，请直接写出△EPC的周长．

Answer 1

【答案】(1)、2cm；(2)、S=12－；(3)、（10+2）cm或（5+）cm．

【解析】

试题分析：(1)、由条件可求得AB=4，BC=6，由勾股定理可求出BD的长；(2)、根据题意得出BQ=x，PD=2x，AQ=4﹣x，AP=6﹣2x，△CPQ的面积S=矩形ABCD的面积﹣△APQ的面积﹣△CDP的面积﹣△BCQ的面积，即可得出结果；(3)、求出CE=6﹣1=5，分三种情况：①当CP=CE=5时，作EM⊥AD于M，则AM=EB=1，EM=AB=4，由勾股定理求出PD，得出PM，再由勾股定理求出PE，即可得出△EPC的周长；

②当PE=CE=5时，同①得：△EPC的周长=10+2；③当PC=PE时，作PN⊥BC于N，则PN=CD=4，EN=CN=CE=2.5，由勾股定理得出PE=PC=，求出△EPC的周长，即可得出结论．

试题解析：(1)、连接BD，如图1所示， ∵+|BC﹣6|=0， ∴AB=4，BC=6，

∴AD=BC=6， 在Rt△ABD中，由勾股定理可求得BD===2（cm）；

(2)、连接CQ、PQ、CP，如图2所示， 根据题意得：BQ=x，PD=2x，AQ=4﹣x，AP=6﹣2x

△CPQ的面积S=矩形ABCD的面积﹣△APQ的面积﹣△CDP的面积﹣△BCQ的面积

=6×4﹣×（6﹣2x）（4﹣x）﹣×2x×4﹣×6×x=12﹣x2（cm2）；

（3）∵BC=6，EB=1， ∴CE=6﹣1=5， 分三种情况： ①当CP=CE=5时，作EM⊥AD于M，如图3所示， 则AM=EB=1，EM=AB=4， ∵∠D=90°，CD=AB=4，

∴PD===3， ∴PM=AD﹣AM﹣PD=6﹣1﹣3=2，

∴PE===2， ∴△EPC的周长=CE+CP+PE=10+2（cm）；

②当PE=CE=5时，同①得：△EPC的周长=10+2（cm）；

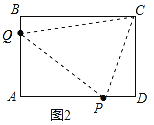
③当PC=PE时，作PN⊥BC于N，如图4所示， 则PN=CD=4，EN=CN=CE=2.5，

∴PE=PC===， ∴△EPC的周长=CE+PC+PE=5+（cm）；

综上所述：△EPC的周长为（10+2）cm或（5+）cm．