题目内容
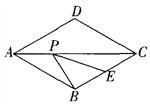
【题目】如图,在菱形ABCD中,AD=8, ![]() ABC=1200,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为_________.
ABC=1200,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为_________.
【答案】4![]() .
.
【解析】试题分析:连接BD,DE,则DE的长即为PE+PB的最小值,再根据菱形ABCD中,∠ABC=120°得出∠BCD的度数,进而判断出△BCD是等边三角形,故△CDE是直角三角形,根据勾股定理即可得出DE的长.
解:连接BD,DE,
∵四边形ABCD是菱形,
∴B、D关于直线AC对称,
∴DE的长即为PE+PB的最小值,
∵ABC=120°,
∴∠BCD=60°,
∴△BCD是等边三角形,
∵E是BC的中点,
∴DE⊥BC,CE=![]() BC=
BC=![]() ×8=4,
×8=4,
∴DE=![]() =
=![]() =4
=4![]() .
.
故答案为:4![]() .
.


练习册系列答案
相关题目