题目内容
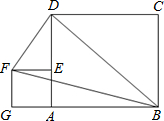 将边长为a的正方形ABCD与边长为b的正方形GHEF如图所示摆放在一起(a≥2b),连接BD,DF,FB,将正方形GHEF绕点A逆时针旋转.在旋转过程中△BDF的面积的取值范围是
将边长为a的正方形ABCD与边长为b的正方形GHEF如图所示摆放在一起(a≥2b),连接BD,DF,FB,将正方形GHEF绕点A逆时针旋转.在旋转过程中△BDF的面积的取值范围是分析:过F作BD的垂线,设垂足为H,由于BD是定值,△BDF的面积最大,则FH最大,△BDF的面积最小,则FH最小;可据此画出图形,求出两种情况下△FDH的面积,从而得到其取值范围.
解答: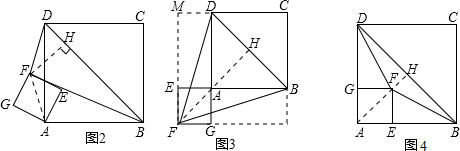
解:∵正方形ABCD的边长为a,正方形GHEF的边长为b,
∴BD=
a,AF=
b,
作FH⊥BD于H点,连接AF.则S△BDF=
×BD×FH(如图2),
因为小正方形AEFG绕A点旋转任意角度,所以点F离线段BD的距离是变化的,即FH的长度是变化的.
由于BD得长度是定值,所以当FH取得最大值时S△BDF最大,当FH取得最小值时S△BDF最小.
所以当点F离BD最远时,FH取得最大值,此时点F、A、H在同一条直线上(如图3所示);
当点F离BD最近时,FH取得最小值,此时点F、A、H也在同一条直线上(如图4所示).
在图3中,S△BDF=
BD×FH=
×
a(
b+
a)=ab+
a2,
在图4中,S△BDF=
BD×FH=
×
a(
a-
b)=
a2-ab,
∴S△BDF的取值范围是:
a2-ab≤S△BDF≤
a2+ab.
故答案为
a2-ab≤S△BDF≤
a2+ab.

解:∵正方形ABCD的边长为a,正方形GHEF的边长为b,
∴BD=
| 2 |
| 2 |
作FH⊥BD于H点,连接AF.则S△BDF=
| 1 |
| 2 |
因为小正方形AEFG绕A点旋转任意角度,所以点F离线段BD的距离是变化的,即FH的长度是变化的.
由于BD得长度是定值,所以当FH取得最大值时S△BDF最大,当FH取得最小值时S△BDF最小.
所以当点F离BD最远时,FH取得最大值,此时点F、A、H在同一条直线上(如图3所示);
当点F离BD最近时,FH取得最小值,此时点F、A、H也在同一条直线上(如图4所示).
在图3中,S△BDF=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
在图4中,S△BDF=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
∴S△BDF的取值范围是:
| 1 |
| 2 |
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了旋转的性质,关键是根据题意,确定旋转中心,旋转方向,旋转角,利用角的和差关系求解.

练习册系列答案
相关题目
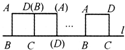 将边长为8cm的正方形ABCD的四边沿直线l向右滚动(不滑动),当正方形滚动两周时,正方形的顶点A所经过的路线的长是( )
将边长为8cm的正方形ABCD的四边沿直线l向右滚动(不滑动),当正方形滚动两周时,正方形的顶点A所经过的路线的长是( )A、(4
| ||
B、(8
| ||
C、(8
| ||
D、(4
|
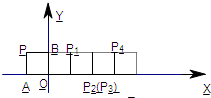 18、如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2008次,点P依次落在点P1,P2,P3,…,P2008的位置,则P2008的横坐标X2008=
18、如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2008次,点P依次落在点P1,P2,P3,…,P2008的位置,则P2008的横坐标X2008=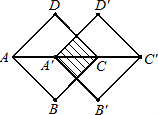 如图,将边长为
如图,将边长为 如图,将边长为12cm的正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为MN.若CE的长为8cm,则MN的长为( )
如图,将边长为12cm的正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为MN.若CE的长为8cm,则MN的长为( ) 将边长为4的正方形在如图的平面直角坐标系中.点P是OA上的一个动点,且从点O向点A运动.连接CP交对角线OB于点D,连接AD.
将边长为4的正方形在如图的平面直角坐标系中.点P是OA上的一个动点,且从点O向点A运动.连接CP交对角线OB于点D,连接AD.