题目内容
 将边长为4的正方形在如图的平面直角坐标系中.点P是OA上的一个动点,且从点O向点A运动.连接CP交对角线OB于点D,连接AD.
将边长为4的正方形在如图的平面直角坐标系中.点P是OA上的一个动点,且从点O向点A运动.连接CP交对角线OB于点D,连接AD.(1)求证:△OCD≌△OAD;
(2)若△OCD的面积是四边形OABC面积的
| 1 | 6 |
(3)若点P从点O运动到点A后,再继续从点A运动到点B,在整个运动过程中,当△OCD恰为等腰三角形时,请直接写出点P的坐标.
分析:(1)根据正方形性质推出OC=OA,∠COD=∠AOD=45°,根据SAS证明三角形全等即可;
(2)求出△OCD的面积是△COB的面积的
,求出OD:BD=1:2,根据相似推出OP:CB=1:2,即可求出OP;
(3)分为三种情况:①OC=OD时,②CD=OD时,③OC=CD时,根据等腰三角形性质和相似求出即可.
(2)求出△OCD的面积是△COB的面积的
| 1 |
| 3 |
(3)分为三种情况:①OC=OD时,②CD=OD时,③OC=CD时,根据等腰三角形性质和相似求出即可.
解答:(1)证明:∵四边形OCBA是正方形,
∴OC=OA,∠COD=∠AOD=45°,
在△OCD和△OAD中
∵
,
∴△OCD≌△OAD(SAS);
(2)解:∵OCD的面积是四边形OABC面积的
,
∴△OCD的面积是△COB的面积的
,
∵△ODC的边OD上的高和△COB的边OB上的高相等,
∴
=
,
∴
=
,
∵四边形OCBA是正方形,
∴OA∥BC,
∴△OPD∽△BCD,
∴
=
=
,
∵BC=4,
∴OP=2,
即P的坐标是(2,0);
(3)解:分为三种情况:①OC=OD时,P点的坐标是(4,8-4
);

②CD=OD时,P点的坐标是(4,0);
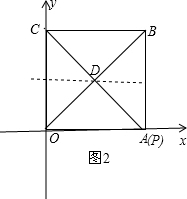
③OC=CD时,P点的坐标是(4,4).
∴OC=OA,∠COD=∠AOD=45°,
在△OCD和△OAD中
∵
|
∴△OCD≌△OAD(SAS);

(2)解:∵OCD的面积是四边形OABC面积的
| 1 |
| 6 |
∴△OCD的面积是△COB的面积的
| 1 |
| 3 |
∵△ODC的边OD上的高和△COB的边OB上的高相等,
∴
| OD |
| OB |
| 1 |
| 3 |
∴
| OD |
| BD |
| 1 |
| 2 |
∵四边形OCBA是正方形,
∴OA∥BC,
∴△OPD∽△BCD,
∴
| OP |
| CB |
| OD |
| BD |
| 1 |
| 2 |
∵BC=4,
∴OP=2,
即P的坐标是(2,0);
(3)解:分为三种情况:①OC=OD时,P点的坐标是(4,8-4
| 2 |

②CD=OD时,P点的坐标是(4,0);

③OC=CD时,P点的坐标是(4,4).

点评:本题考查了正方形性质,相似三角形的性质和判定,等腰三角形的性质等知识点的综合运用.

练习册系列答案
相关题目
 8、如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2012次,点P依次落在点P1,P2,P3,P4,…,P2012的位置,则P2012的横坐标x2012=( )
8、如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2012次,点P依次落在点P1,P2,P3,P4,…,P2012的位置,则P2012的横坐标x2012=( )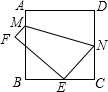 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN的长是
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN的长是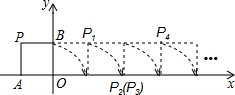 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转8次,点P依次落在点P1、P2、P3、P4、P8的位置,则P8的横坐标是( )
如图,将边长为1的正方形OAPB沿x轴正方向连续翻转8次,点P依次落在点P1、P2、P3、P4、P8的位置,则P8的横坐标是( )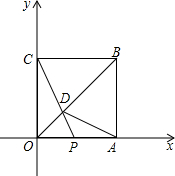 将边长为4的正方形在如图的平面直角坐标系中.点P是OA上的一个动点,且从点O向点A运动.连接CP交对角线OB于点D,连接AD.
将边长为4的正方形在如图的平面直角坐标系中.点P是OA上的一个动点,且从点O向点A运动.连接CP交对角线OB于点D,连接AD. ,求P点的坐标;
,求P点的坐标;