题目内容
(2012•鞍山二模)如果给你一副带有刻度的三角板,请你画出以∠AOB为一内角的菱形.下面一位同学是这样设计的.分别在OA,OB上量取OM=ON,连接MN;取MN的中点P:作射线OP,截取QP=OP,那么四边形MQNO是菱形.
(1)这位同学的设计你认为正确吗?若正确,请对正确做法加以证明;若不正确,请简要说明理由.
(2)请你根据以上信息,创造新的菱形的作法,在备用图上画出图形,并证明其可行性.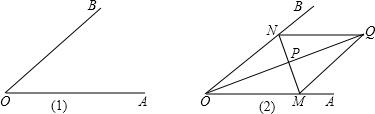
(1)这位同学的设计你认为正确吗?若正确,请对正确做法加以证明;若不正确,请简要说明理由.
(2)请你根据以上信息,创造新的菱形的作法,在备用图上画出图形,并证明其可行性.

分析:(1)首先根据等腰三角形的性质可得PO⊥MN,PN=PM,再有条件OP=PQ可根据对角线互相垂直平分的四边形是菱形判断出四边形MQNO是菱形;
(2)根据对角线垂直且互相平分的四边形是菱形画图即可.
(2)根据对角线垂直且互相平分的四边形是菱形画图即可.
解答:解:(1)正确.理由如下:
∵OM=ON,P是MN的中点,
∴PO⊥MN,PN=PM,
∵OP=PQ,
∴四边形MQNO是菱形;
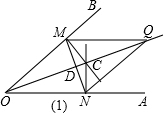
(2)如图所示:分别在OA,OB上量取OM=ON;连接MN
过点M,N分别作OA,OB的垂线相交于点C;
作射线OC,交MN于点D,截取QD=OD,
那么四边形MQNO是菱形.
∵OM=ON,P是MN的中点,
∴PO⊥MN,PN=PM,
∵OP=PQ,
∴四边形MQNO是菱形;

(2)如图所示:分别在OA,OB上量取OM=ON;连接MN
过点M,N分别作OA,OB的垂线相交于点C;
作射线OC,交MN于点D,截取QD=OD,
那么四边形MQNO是菱形.
点评:此题主要考查了菱形的判定,以及作图,关键是熟练掌握菱形的判定定理:菱形定义:一组邻边相等的平行四边形是菱形(平行四边形+一组邻边相等=菱形);四条边都相等的四边形是菱形.对角线互相垂直的平行四边形是菱形(或“对角线互相垂直平分的四边形是菱形”).

练习册系列答案
相关题目
 (2012•鞍山二模)在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长,与BC的延长线交于点F,连接OE.求证:
(2012•鞍山二模)在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长,与BC的延长线交于点F,连接OE.求证: (2012•鞍山二模)如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60°.
(2012•鞍山二模)如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60°. (2012•鞍山二模)函数y=kx+b的图象如图所示,当y<0时,x的取值范围是
(2012•鞍山二模)函数y=kx+b的图象如图所示,当y<0时,x的取值范围是 (2012•鞍山二模)如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N.P、Q分别是
(2012•鞍山二模)如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N.P、Q分别是
 点A出发以每秒2个单位的速度沿直线l1向左上方匀速运动,设它们运动时间为t.
点A出发以每秒2个单位的速度沿直线l1向左上方匀速运动,设它们运动时间为t.