Question

（2012•鞍山二模）如图，AB是⊙O的直径，M是⊙O上一点，MN⊥AB，垂足为N．P、Q分别是

AM

、

BM

上一点（不与端点重合），如果∠MNP=∠MNQ，求证：MN²=PN•QN．

Answer 1

分析：延长QN交圆O于C，延长MN交圆O于D，如图所示，由MN垂直于AB，得到一对直角相等，再由已知的一对角相等，得到∠1=∠2，由MN垂直于AB，利用垂径定理得到A为弧DM的中点，再由一对对顶角相等，得到∠1=∠ANC，可得出P与C关于AB对称，进而得到弧PA=弧AC，利用等式的性质得到弧PD=弧MC，利用等弧所对的圆周角相等得到一对角相等，再由已知的一对角相等，利用两对对应角相等的两三角形相似，得到三角形PMN与三角形MNQ相似，由相似得比例，即可得证．

解答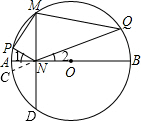：解：延长QN交圆O于C，延长MN交圆O于D，如图所示，
∵MN⊥AB，∠MNP=∠MNQ，
∴∠1=∠2，
∵AB是⊙O的直径，MN⊥AB，
∴

AM

=

DA

，
∵∠1=∠2，∠ANC=∠2，
∴∠1=∠ANC，
∴P，C关于AB对称，
∴

PA

=

AC

，

PD

=

MC

，
∴∠Q=∠PMN，
又∵∠MNP=∠MNQ，
∴△PMN∽△MQN，
∴MN²=PN•QN．

点评：此题考查了垂径定理、圆周角定理、相似三角形的判定与性质以及等腰三角形的性质等知识．此题综合性较强，难度适中，解题的关键是注意数形结合思想的应用，注意辅助线的作法．