题目内容
 (2012•鞍山二模)在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长,与BC的延长线交于点F,连接OE.求证:
(2012•鞍山二模)在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长,与BC的延长线交于点F,连接OE.求证:(1)BD=BF;
(2)∠EOD=2∠AED.
分析:(1)根据切线性质得出OE⊥AC,推出OE∥BC,推出∠OED=∠F,根据等腰三角形性质推出∠ODE=∠OED,推出∠ODE=∠F即可;
(2)根据的切线的性质∠OEA=90°,推出∠AED+∠DEO=90°①,根据等腰三角形性质和三角形的内角和定理求出∠DOE=180°-2∠DEO,推出
∠DOE+∠DEO=90°②,由①②即可求出答案.
(2)根据的切线的性质∠OEA=90°,推出∠AED+∠DEO=90°①,根据等腰三角形性质和三角形的内角和定理求出∠DOE=180°-2∠DEO,推出
| 1 |
| 2 |
解答:(1)证明:∵AC切⊙O于E,
∴OE⊥AC,
∵∠ACB=90°,
∴AC⊥BC,
∴OE∥BC,
∴∠OED=∠F,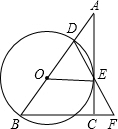
∵OD=OE,
∴∠ODE=∠OED,
∴∠ODE=∠F,
∴BD=BF;
(2)∵AC是⊙O的切线,
∴∠OEA=90°,
即∠AED+∠DEO=90°①,
∵OE=OD,
∴∠EDO=∠DEO,
∴∠DOE=180°-2∠DEO,
即
∠DOE+∠DEO=90°②,
由①②得:∠AED-
∠DOE=0,
则∠DOE=2∠AED.
∴OE⊥AC,
∵∠ACB=90°,
∴AC⊥BC,
∴OE∥BC,
∴∠OED=∠F,

∵OD=OE,
∴∠ODE=∠OED,
∴∠ODE=∠F,
∴BD=BF;
(2)∵AC是⊙O的切线,
∴∠OEA=90°,
即∠AED+∠DEO=90°①,
∵OE=OD,
∴∠EDO=∠DEO,
∴∠DOE=180°-2∠DEO,
即
| 1 |
| 2 |
由①②得:∠AED-
| 1 |
| 2 |
则∠DOE=2∠AED.
点评:本题综合考查了切线的性质,平行线的性质和判定,等腰三角形的性质和判定,三角形的内角和定理等知识点,主要考查学生的推理能力,本题综合性比较强,有一定的难度.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 (2012•鞍山二模)如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60°.
(2012•鞍山二模)如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60°. (2012•鞍山二模)函数y=kx+b的图象如图所示,当y<0时,x的取值范围是
(2012•鞍山二模)函数y=kx+b的图象如图所示,当y<0时,x的取值范围是 (2012•鞍山二模)如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N.P、Q分别是
(2012•鞍山二模)如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N.P、Q分别是
 点A出发以每秒2个单位的速度沿直线l1向左上方匀速运动,设它们运动时间为t.
点A出发以每秒2个单位的速度沿直线l1向左上方匀速运动,设它们运动时间为t.