Question

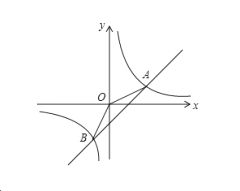
【题目】如图，一次函数的图象交轴于点，交轴于点，点在线段上（不与点，重合）过点分別作和的垂线，垂足为，．

（1）关于矩形面积的探究：

①点在何处时，矩形的面积为1？写出计算过程；

②是否存在一点，能使矩形的面积为？说说你的理由．

（2）设点的坐标是，，图中阴影部分的面积为，尝试完成下列问题：

①建立与的关系式，并类比一次函数猜想是的什么函数，能否对此类函数下一个描述性的定义，其中包含它的一般形式；

②我们知道代数式有最小值9，试问当在何处时有最小值，请把你的理由．

Answer 1

【答案】（1）①当或，时，矩形的面积为1；②不存在一点，能使矩形的面积为；理由见解析；（2）①，它是二次函数，若两个变量，的对应关系可以表示，，是常数，的形式，则称是的二次函数；②当，时，有最小值．

【解析】

（1）①可设，，则矩形的面积可表示为，令其等于1，解方程即可. ②令矩形的面积表达式等于，解方程看是否有解即可.

（2）①观察图形可知，阴影部分面积等于的面积减去矩形的面积，代入数值计算整理为函数的一般形式即可. ②把第①问里的二次函数整理变形为顶点式，根据二次函数的性质求最值即可.

（1）点在线段上，

设，，

①由题意得，，

解得：，，

或，

综上所述，当或，时，矩形的面积为1；

②由题意得，，

整理得，，

△，此方程无实数根，

不存在一点，能使矩形的面积为；

（2）①一次函数的图象交轴于点，交轴于点，

，，，

，

它是二次函数，类比得到一般的，若两个变量，的对应关系可以表示，，是常数，的形式，则称是的二次函数；

②，

当时，有最小值，

当，时，有最小值．