题目内容
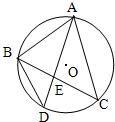 21、如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交边BC于点E,连接BD.
21、如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交边BC于点E,连接BD.(1)根据题设条件,请你找出图中各对相似三角形;
(2)请选择其中的一对相似三角形加以证明.
分析:认真审题,选择适宜的相似三角形的判定方法进行判定.
解答:解:△DBE∽△DAB;△DBE∽△CAE;△ABD∽△AEC各(1分)共(3分)
选择△ABD∽△AEC.
∵DA是∠BAC的平分线,
∴∠BAD=∠CAE.(4分)
∵∠D=∠C,(6分)
∴△ABD∽△AEC.(8分)
选择△ABD∽△AEC.
∵DA是∠BAC的平分线,
∴∠BAD=∠CAE.(4分)
∵∠D=∠C,(6分)
∴△ABD∽△AEC.(8分)
点评:此题考查了相似三角形的判定:
①有两个对应角相等的三角形相似;
②有两个对应边的比相等,且其夹角相等,则两个三角形相似;
③三组对应边的比相等,则两个三角形相似.
①有两个对应角相等的三角形相似;
②有两个对应边的比相等,且其夹角相等,则两个三角形相似;
③三组对应边的比相等,则两个三角形相似.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD=
15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD= 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.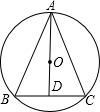 已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积.
已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积. 18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( )
18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( ) 如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.
如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.