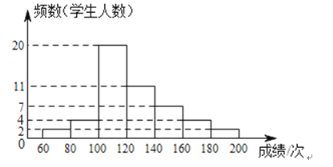
Ő‚ńŅńŕ»›
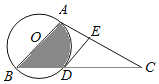
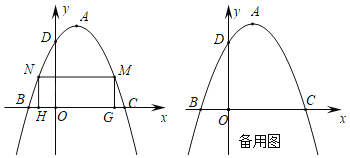
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“—÷™∂ĢīőļĮ żÕľŌůĶń∂•Ķ„◊ÝĪÍő™A£®1£¨4£©£¨”Ž◊ÝĪÍ÷ŠĹĽ”ŕB°ĘC°ĘD»żĶ„£¨«“BĶ„Ķń◊ÝĪÍő™£®©Ā1£¨0£©£ģ
£®1£©«ů∂ĢīőļĮ żĶńĹ‚őŲ Ĺ£Ľ
£®2£©‘ŕ∂ĢīőļĮ żÕľŌůőĽ”ŕx÷Š…Ō∑Ĺ≤Ņ∑÷”–ŃĹłŲ∂ĮĶ„M°ĘN£¨«“Ķ„N‘ŕĶ„MĶń◊ů≤ŗ£¨ĻżM°ĘN◊ųx÷ŠĶńīĻŌŖĹĽx÷Š”ŕĶ„G°ĘHŃĹĶ„£¨ĶĪňńĪŖ–őMNHGő™ĺō–ő Ī£¨«ůł√ĺō–ő÷‹≥§Ķń◊Óīů÷Ķ£Ľ
£®3£©ĶĪĺō–őMNHGĶń÷‹≥§◊Óīů Ī£¨ń‹∑Ů‘ŕ∂ĢīőļĮ żÕľŌů…Ō’“ĶĹ“ĽĶ„P£¨ Ļ°ųPNCĶń√śĽż «ĺō–őMNHG√śĽżĶń![]() £Ņ»Űīś‘ŕ£¨«ů≥Ųł√Ķ„ĶńļŠ◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
£Ņ»Űīś‘ŕ£¨«ů≥Ųł√Ķ„ĶńļŠ◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ£®1£©y£Ĺ©Āx2+2x+3 £®2£©10 £®3£©īś‘ŕ£Ľ£®![]() £¨
£¨![]() £©ĽÚ£®
£©ĽÚ£®![]() £¨
£¨![]() £©ĽÚ£®
£©ĽÚ£®![]() £¨
£¨![]() £©
£©
°ĺĹ‚őŲ°Ņ
£®1£©ĹęŇ◊őÔŌŖĶńĹ‚őŲ Ĺ…Ťő™∂•Ķ„ Ĺ£¨»ĽļůĹęĶ„Bīķ»ŽľīŅ…«ů≥ŲŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£®2£©”…ňńĪŖ–őMNHGő™ĺō–ő÷™MN°őx÷Š£¨MG°őy÷Š£¨Ļ Ņ……Ť≥ŲĶ„M◊ÝĪÍ£¨‘Úĺō–őMNHGĶń÷‹≥§C£Ĺ2MN+2GM£Ĺ2£®2x©Ā2£©+2£®©Āx2+2x+3£©£Ĺ©Ā2x2+8x+2£¨ņŻ”√∂ĢīőļĮ ż–‘÷ ľīŅ…«ůĹ‚£Ľ
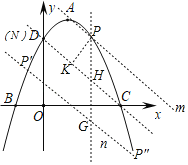
£®3£©”…£®2£©÷–÷™£¨D”ŽN÷ōļŌ£¨”…“—÷™Ō»«ů≥ŲS°ųPNC÷Ķ£¨Ń¨Ĺ”DC£¨‘ŕCDĶ√…ŌŌ¬∑ĹĶ»ĺŗņŽī¶◊ųCDĶń∆Ĺ––ŌŖm°Ęn£¨ĻżĶ„P◊ųy÷ŠĶń∆Ĺ––ŌŖĹĽCD°Ę÷ĪŌŖn”ŕĶ„H°ĘG£¨ľīPH£ĹGH£¨ĻżĶ„P◊ųPK°ÕCD”ŕĶ„K£¨…Ť≥ŲĶ„P◊ÝĪÍ£¨Õ®ĻżÕ∆Ķľľ∆ň„£¨ľīŅ…«ůĹ‚≥ŲĶ„PĶń◊ÝĪÍ.
£®1£©∂ĢīőļĮ żĪŪīÔ Ĺő™£ļy£Ĺa£®x©Ā1£©2+4£¨
ĹęĶ„BĶń◊ÝĪÍīķ»Ž…Ō ĹĶ√£ļ0£Ĺ4a+4£¨Ĺ‚Ķ√£ļa£Ĺ©Ā1£¨
Ļ ļĮ żĪŪīÔ Ĺő™£ļy£Ĺ©Āx2+2x+3°≠ĘŔ£Ľ
£®2£©…ŤĶ„MĶń◊ÝĪÍő™£®x£¨©Āx2+2x+3£©£¨‘ÚĶ„N£®2©Āx£¨©Āx2+2x+3£©£¨
‘ÚMN£Ĺx©Ā2+x£Ĺ2x©Ā2£¨GM£Ĺ©Āx2+2x+3£¨
ĺō–őMNHGĶń÷‹≥§C£Ĺ2MN+2GM£Ĺ2£®2x©Ā2£©+2£®©Āx2+2x+3£©£Ĺ©Ā2x2+8x+2£¨
°Ŗ©Ā2£ľ0£¨Ļ ĶĪx£Ĺ![]() £Ĺ2£¨C”–◊Óīů÷Ķ£¨◊Óīů÷Ķő™10£¨
£Ĺ2£¨C”–◊Óīů÷Ķ£¨◊Óīů÷Ķő™10£¨
īň Īx£Ĺ2£¨Ķ„N£®0£¨3£©”ŽĶ„D÷ōļŌ£Ľ
£®3£©°ųPNCĶń√śĽż «ĺō–őMNHG√śĽżĶń![]() £¨
£¨
‘ÚS°ųPNC£Ĺ![]() °ŃMN°ŃGM£Ĺ
°ŃMN°ŃGM£Ĺ![]() °Ń2°Ń3£Ĺ
°Ń2°Ń3£Ĺ![]() £¨
£¨
ѨŔDC£¨‘ŕCDĶ√…ŌŌ¬∑ĹĶ»ĺŗņŽī¶◊ųCDĶń∆Ĺ––ŌŖm°Ęn£¨ĻżĶ„P◊ųy÷ŠĶń∆Ĺ––ŌŖĹĽCD°Ę÷ĪŌŖn”ŕĶ„H°ĘG£¨ľīPH£ĹGH£¨ĻżĶ„P◊ųPK°ÕCD”ŕĶ„K£¨
ĹęC£®3£¨0£©°ĘD£®0
÷ĪŌŖCDĶńĪŪīÔ Ĺő™£ļy£Ĺ©Āx+3£¨
OC£ĹOD£¨°ŗ°ŌOCD£Ĺ°ŌODC£Ĺ45°„£Ĺ°ŌPHK£¨CD£Ĺ3![]() £¨
£¨
…ŤĶ„P£®x£¨©Āx2+2x+3£©£¨‘ÚĶ„H£®x£¨©Āx+3£©£¨
S°ųPNC£Ĺ![]() £Ĺ
£Ĺ![]() °ŃPK°ŃCD£Ĺ
°ŃPK°ŃCD£Ĺ![]() °ŃPH°Ńsin45°„°Ń3
°ŃPH°Ńsin45°„°Ń3![]() £¨
£¨
Ĺ‚Ķ√£ļPH£Ĺ![]() £ĹHG£¨
£ĹHG£¨
‘ÚPH£Ĺ©Āx2+2x+3+x©Ā3£Ĺ![]() £¨
£¨
Ĺ‚Ķ√£ļx£Ĺ![]() £¨
£¨
Ļ Ķ„P£®![]() £¨
£¨![]() £©£¨
£©£¨
÷ĪŌŖnĶńĪŪīÔ Ĺő™£ļy£Ĺ©Āx+3©Ā![]() £Ĺ©Āx+
£Ĺ©Āx+![]() °≠Ęŕ£¨
°≠Ęŕ£¨
Ń™ŃĘĘŔĘŕ≤ĘĹ‚Ķ√£ļx£Ĺ![]() £¨
£¨
ľīĶ„P°š°ĘP°ŚĶń◊ÝĪÍ∑÷Īūő™(![]() £¨
£¨![]() £©°Ę£®
£©°Ę£®![]() £¨
£¨![]() £©£Ľ
£©£Ľ
Ļ Ķ„P◊ÝĪÍő™£ļ£®![]() £¨
£¨![]() £©ĽÚ£®
£©ĽÚ£®![]() £¨
£¨![]() £©ĽÚ£®
£©ĽÚ£®![]() £¨
£¨![]() £©.
£©.

 ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł
ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł –°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
–°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņ…ĹĶō◊‘––≥Ķ‘Ĺņī‘Ĺ ‹ńÍ«Š»ňĶńŌ≤įģ£ģń≥≥Ķ––ĺ≠”™ĶńA–Õ…ĹĶō◊‘––≥Ķ»•ńÍŌķ Ř◊‹∂Óő™30ÕÚ‘™£¨ĹŮńÍ√ŅŃĺ≥Ķ ŘľŘĪ»»•ńÍĹĶĶÕŃň200‘™£ģ»Ű¬Ű≥ŲĶń żŃŅŌŗÕ¨£¨Ōķ Ř◊‹∂ÓĹęĪ»»•ńÍľű…Ŕ10%£¨
£®1£©ĹŮńÍA–Õ≥Ķ√ŅŃĺ ŘľŘ∂ŗ…Ŕ‘™£Ņ
£®2£©ł√≥Ķ––ľ∆Ľģ‘ŔĹÝ“ĽŇķA–Õ≥ĶļÕ–¬ŅÓB–Õ≥ĶĻ≤60Ńĺ£¨“™ Ļ’‚Ňķ≥ĶĽŮņŻ≤Ľ…Ŕ”ŕ4ÕÚ‘™£¨A–Õ≥Ķ÷Ń∂ŗĹÝ∂ŗ…ŔŃĺ£Ņ
A°ĘBŃĹ÷÷–ÕļŇ≥ĶĶńĹÝĽűļÕŌķ ؾسٻÁĪŪ£ļ
A–Õ≥Ķ | B–Õ≥Ķ | |
ĹÝĽűľŘłŮ£®‘™£© | 1200 | 1400 |
Ōķ ŘľŘłŮ£®‘™£© | ĹŮńÍĶńŌķ ؾس٠| 2200 |