题目内容
如图,已知直角梯形ABCD中,AD∥BC,ÐB=90º,ÐC=60º, BC=12cm,DC=16cm,动点P沿A→D→C线路以2cm/秒的速度向C运动,动点Q沿B→C线路以1cm/秒的速度向C运动。P、Q两点分别从A、B同时出发,当其中一点到达C点时,另一点也随之停止。设运动时间为t秒,△PQB的面积为y cm2。

(1)求AD的长及t的取值范围;
(2)求y关于t的函数关系式;
(3)是否存在这样的t,使得△PQB的面积为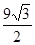
【答案】
(1)AD=4㎝ 0≤t≤10
(2)当0≤t≤2时, 当2<t≤10时,
当2<t≤10时,
(3)当0≤t≤2时,t= ;当2<t≤10时,t=9
;当2<t≤10时,t=9
【解析】(1)过D作DE⊥BC于E点,把梯形的问题转化为矩形和直角三角形的问题,结合题目的已知条件,利用勾股定理即可求出CE,然后也可以求出AD的长度,接着就可以求出点P从出发到点C和点Q从出发到点C所需时间,也就求出了t的取值范围;
(2)首先通过计算确定P的位置在点P在DC边上,过点P作PM⊥BC于M,由此得到PM∥DE,然后利用平行线分线段成比例可以用t表示PM,再利用三角形的面积公式即可求出函数关系式;
(3)利用函数关系式结合t的取值范围把△PQB的面积为 代入函数的解析式,即可求出t的值.
代入函数的解析式,即可求出t的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知直角梯形ABCD中,AD∥BC∥EF,∠A=90°,BC=DC=4,AC、BD交于E,且EF=ED.
如图,已知直角梯形ABCD中,AD∥BC∥EF,∠A=90°,BC=DC=4,AC、BD交于E,且EF=ED. 21、当我们遇到梯形问题时,我们常用分割的方法,将其转化成我们熟悉的图形来解决:
21、当我们遇到梯形问题时,我们常用分割的方法,将其转化成我们熟悉的图形来解决:
 如图,已知直角梯形的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形的中位线长为 ( )
如图,已知直角梯形的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形的中位线长为 ( ) 如图,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.点E是CD的中点,点F是AB上的点,∠ADF=45°,FE=a,梯形ABCD的面积为m.
如图,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.点E是CD的中点,点F是AB上的点,∠ADF=45°,FE=a,梯形ABCD的面积为m. 如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,∠C=60°,BC=12cm,DC=16cm,动点P沿A→D→C线路以2cm/秒的速度向C运动,动点Q沿B→C线路以1cm/秒的速度向C运动.P、Q两点分别从A、B同时出发,当其中一点到达C点时,另一点也随之停止.设运动时间为t秒,△PQB的面积为y cm2.
如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,∠C=60°,BC=12cm,DC=16cm,动点P沿A→D→C线路以2cm/秒的速度向C运动,动点Q沿B→C线路以1cm/秒的速度向C运动.P、Q两点分别从A、B同时出发,当其中一点到达C点时,另一点也随之停止.设运动时间为t秒,△PQB的面积为y cm2.