题目内容
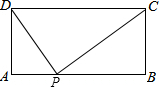
如图，在矩形ABCD中，AB=10，AD=4，点P是边AB上一点，若△APD与△BPC相似，则满足条件的点P有______个．
设AP为x，
∵AB=10，
∴PB=10-x，
①AD和PB是对应边时，
∵△APD与△BPC相似，
∴
=
，
即
=
，
整理得，x2-10x+16=0，
解得x1=2，x2=8，
②AD和BC是对应边时，
∵△APD与△BPC相似，
∴
=
，
即
=
，
解得x=5，
所以，当AP=2、5、8时，△APD与△BPC相似，
满足条件的点P有3个．
故答案为：3．
∵AB=10，
∴PB=10-x，
①AD和PB是对应边时，
∵△APD与△BPC相似，
∴
| AD |
| PB |
| AP |
| BC |
即
| 4 |
| 10-x |
| x |
| 4 |
整理得，x2-10x+16=0，
解得x1=2，x2=8，
②AD和BC是对应边时，
∵△APD与△BPC相似，
∴
| AD |
| BC |
| AP |
| PB |
即
| 4 |
| 4 |
| x |
| 10-x |
解得x=5，
所以，当AP=2、5、8时，△APD与△BPC相似，
满足条件的点P有3个．
故答案为：3．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
