题目内容
 如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=
如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=
- A.8
- B.6
- C.4
- D.3
C
分析:可过点P作平行四边形PGBD,EPHC,进而利用平行四边形的性质及等边三角形的性质即可求解此题.
解答: 解:延长EP、FP分别交AB、BC于G、H,
解:延长EP、FP分别交AB、BC于G、H,
则由PD∥AB,PE∥BC,PF∥AC,可得,
四边形PGBD,EPHC是平行四边形,
∴PG=BD,PE=HC,
又△ABC是等边三角形,
又有PF∥AC,PD∥AB可得△PFG,△PDH是等边三角形,
∴PF=PG=BD,PD=DH,
又△ABC的周长为12,
∴PD+PE+PF=DH+HC+BD=BC= ×12=4,
×12=4,
故应选C.
点评:本题主要考查了平行四边形的判定及性质以及等边三角形的判定及性质,应熟练掌握.
分析:可过点P作平行四边形PGBD,EPHC,进而利用平行四边形的性质及等边三角形的性质即可求解此题.
解答:
 解:延长EP、FP分别交AB、BC于G、H,
解:延长EP、FP分别交AB、BC于G、H,则由PD∥AB,PE∥BC,PF∥AC,可得,
四边形PGBD,EPHC是平行四边形,
∴PG=BD,PE=HC,
又△ABC是等边三角形,
又有PF∥AC,PD∥AB可得△PFG,△PDH是等边三角形,
∴PF=PG=BD,PD=DH,
又△ABC的周长为12,
∴PD+PE+PF=DH+HC+BD=BC=
 ×12=4,
×12=4,故应选C.
点评:本题主要考查了平行四边形的判定及性质以及等边三角形的判定及性质,应熟练掌握.

练习册系列答案
相关题目
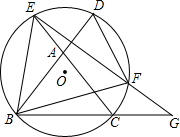 ∥AC,EF的延长线交BC的延长线于点G.
∥AC,EF的延长线交BC的延长线于点G. 9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角
9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角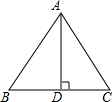 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于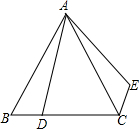 如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是
如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是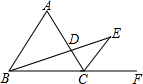 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.