题目内容
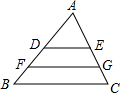 如图,已知DE是△ABC的一条中位线,F、G分别是线段BD、CE的中点,若FG=6,则BC=
如图,已知DE是△ABC的一条中位线,F、G分别是线段BD、CE的中点,若FG=6,则BC=8
8
.分析:由DE为三角形ABC的中位线,根据三角形的中位线平行于第三条边,且等于第三条边的一半,得到DE等于BC的一半,DE与BC平行,又BD与CE交于点A,故四边形BCED为梯形,又F和G分别为两腰的中点,可得FG为梯形的中位线,根据梯形中位线定理,梯形的中位线平行于底边,且等于上下底之和的一半,得到FG与BC的关系式,把FG的长代入即可求出BC的长.
解答:解:∵DE是△ABC的中位线,
∴DE=
BC,且DE∥BC,
又BD与CE相交于点A,
∴四边形BCED为梯形,
又F、G分别是线段BD、CE的中点,
∴FG为梯形BCED的中位线,
∴FG=
(DE+BC)=
(
BC+BC)=
BC,
∵FG=6,
∴BC=
×6=8.
故答案为:8
∴DE=
| 1 |
| 2 |
又BD与CE相交于点A,
∴四边形BCED为梯形,
又F、G分别是线段BD、CE的中点,
∴FG为梯形BCED的中位线,
∴FG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
∵FG=6,
∴BC=
| 4 |
| 3 |
故答案为:8
点评:此题考查了三角形中位线定理,梯形的判定以及梯形的中位线定理,其中三角形的中位线定理为:三角形的中位线平行于第三边,且等于第三边的一半;梯形的中位线定理为:梯形的中位线平行于底边,且等于上下底之和的一半.同时本题还利用了转化的数学思想,达到了解题的目的.

练习册系列答案
相关题目
 17、如图,已知DE是AC的垂直平分线,AB=10cm,BC=11cm,则△ABD的周长为
17、如图,已知DE是AC的垂直平分线,AB=10cm,BC=11cm,则△ABD的周长为 如图,已知DE是直角梯形ABCD的高,将△ADE沿DE翻折,腰AD恰好经过腰BC的中点,则AE:BE等于( )
如图,已知DE是直角梯形ABCD的高,将△ADE沿DE翻折,腰AD恰好经过腰BC的中点,则AE:BE等于( )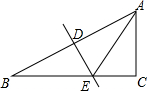 30°.
30°.