题目内容
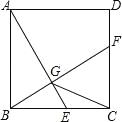
【题目】(1)问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证:AD![]() BC=AP
BC=AP![]() BP.
BP.
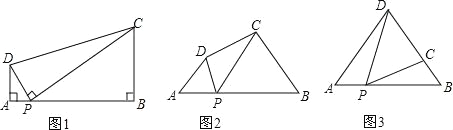
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=12,AD=BD=10.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.
【答案】(1)证明见解析;(2)结果成立,理由见解析;(3)t的值为2秒或10秒.
【解析】
试题分析:(1)由∠DPC=∠A=∠B=90°可得∠ADP=∠BPC,即可证到△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;
(2)由∠DPC=∠A=∠B=θ可得∠ADP=∠BPC,即可证到△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;
(3)过点D作DE⊥AB于点E,根据等腰三角形的性质可得AE=BE=6,根据勾股定理可得DE=8,由题可得DC=DE=8,则有BC=10-8=2.易证∠DPC=∠A=∠B.根据AD![]() BC=AP
BC=AP![]() BP,就可求出t的值.
BP,就可求出t的值.
试题解析:(1)如图1,
∵∠DPC=∠A=∠B=90°,
∴∠ADP+∠APD=90°,
∠BPC+∠APD=90°,
∴∠APD=∠BPC,
∴△ADP∽△BPC,
∴![]() ,
,
∴AD![]() BC=AP
BC=AP![]() BP;
BP;
(2)结论AD![]() BC=AP
BC=AP![]() BP仍成立;
BP仍成立;
证明:如图2,∵∠BPD=∠DPC+∠BPC,
又∵∠BPD=∠A+∠APD,
∴∠DPC+∠BPC=∠A+∠APD,
∵∠DPC=∠A=θ,
∴∠BPC=∠APD,
又∵∠A=∠B=θ,
∴△ADP∽△BPC,
∴![]() ,
,
∴AD![]() BC=AP
BC=AP![]() BP;
BP;
(3)如下图,过点D作DE⊥AB于点E,
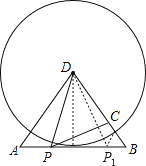
∵AD=BD=10,AB=12,
∴AE=BE=6
∴DE=![]() =8,
=8,
∵以D为圆心,以DC为半径的圆与AB相切,
∴DC=DE=8,
∴BC=10-8=2,
∵AD=BD,
∴∠A=∠B,
又∵∠DPC=∠A,
∴∠DPC=∠A=∠B,
由(1)(2)的经验得ADBC=APBP,
又∵AP=t,BP=12-t,
∴t(12-t)=10×2,
∴t=2或t=10,
∴t的值为2秒或10秒.