题目内容
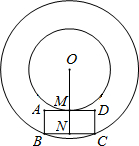 26、如图,以点O为圆心的两个同心圆中,矩形ABCD的边BC为大圆的弦,边AD与小圆相切于点M,OM的延长线与BC相交于点N.
26、如图,以点O为圆心的两个同心圆中,矩形ABCD的边BC为大圆的弦,边AD与小圆相切于点M,OM的延长线与BC相交于点N.(1)点N是线段BC的中点吗?为什么?
(2)若圆环的宽度(两圆半径之差)为6cm,AB=5cm,BC=10cm,求小圆的半径.
分析:(1)由AD是小圆的切线可知OM⊥AD,再由四边形ABCD是矩形可知,AD∥BC,AB=CD,故ON⊥BC,由垂径定理即可得出结论;
(2)延长ON交大圆于点E,由于圆环的宽度(两圆半径之差)为6cm,AB=5cm可知ME=6cm,在Rt△OBE中,利用勾股定理即可求出OM的长.
(2)延长ON交大圆于点E,由于圆环的宽度(两圆半径之差)为6cm,AB=5cm可知ME=6cm,在Rt△OBE中,利用勾股定理即可求出OM的长.
解答: 解:(1)∵AD是小圆的切线,M为切点,
解:(1)∵AD是小圆的切线,M为切点,
∴OM⊥AD,
∵四边形ABCD是矩形,
∴AD∥BC,
∴ON⊥BC,
∴N是BC的中点;
(2)延长ON交大圆于点E,
∵圆环的宽度(两圆半径之差)为6cm,AB=5cm,
∴ME=6cm,
在Rt△OBN中,设OM=r,
OB2=BN2+(OM+MN)2,
即(r+6)2=52+(r+5)2,
解得r=7cm,
故小圆半径为7cm.
 解:(1)∵AD是小圆的切线,M为切点,
解:(1)∵AD是小圆的切线,M为切点,∴OM⊥AD,
∵四边形ABCD是矩形,
∴AD∥BC,
∴ON⊥BC,
∴N是BC的中点;
(2)延长ON交大圆于点E,
∵圆环的宽度(两圆半径之差)为6cm,AB=5cm,
∴ME=6cm,
在Rt△OBN中,设OM=r,
OB2=BN2+(OM+MN)2,
即(r+6)2=52+(r+5)2,
解得r=7cm,
故小圆半径为7cm.
点评:本题考查的是垂径定理,涉及到切线的性质及勾股定理、矩形的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
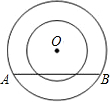 如图,以点O为圆心的两个同心圆,半径分别为5和3,若大圆的弦AB与小圆相交,则弦长AB的取值范围是( )
如图,以点O为圆心的两个同心圆,半径分别为5和3,若大圆的弦AB与小圆相交,则弦长AB的取值范围是( )| A、8≤AB≤10 | B、AB≥8 | C、8<AB≤10 | D、8<AB<10 |
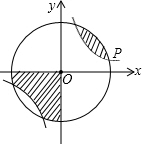 如图,以点O为圆心的圆与反比例函数的图象相交,若其中一个交点P的坐标为(5,1),则图中两块阴影部分的面积和为
如图,以点O为圆心的圆与反比例函数的图象相交,若其中一个交点P的坐标为(5,1),则图中两块阴影部分的面积和为 12、如图,以点P为圆心的圆弧与x轴交于A,B两点,点P的坐标为(4,2),点A的坐标为(2,0),则点B的坐标为
12、如图,以点P为圆心的圆弧与x轴交于A,B两点,点P的坐标为(4,2),点A的坐标为(2,0),则点B的坐标为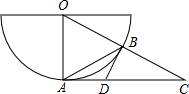 如图是以点O为圆心的半圆,AB是半圆的一条弦,延长OB与过点A的直线交于点C,AB=BC=OB.
如图是以点O为圆心的半圆,AB是半圆的一条弦,延长OB与过点A的直线交于点C,AB=BC=OB.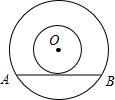 如图,以点O为圆心的两个同心圆,当大圆的弦AB与小圆相切时弦长AB=8,则这两个同心圆所形成的圆环的面积是
如图,以点O为圆心的两个同心圆,当大圆的弦AB与小圆相切时弦长AB=8,则这两个同心圆所形成的圆环的面积是