题目内容
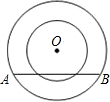如图，以点O为圆心的两个同心圆，半径分别为5和3，若大圆的弦AB与小圆相交，则弦长AB的取值范围是（ ）| A、8≤AB≤10 | B、AB≥8 | C、8＜AB≤10 | D、8＜AB＜10 |
分析：要求弦长AB的取值范围，则只需求得弦的最小值和弦的最大值．根据直线和圆相切时，运用垂径定理和勾股定理进行求解，求得弦的最小值；根据直径是圆中最长的弦，求得弦长的最大值．
解答：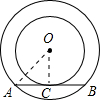
解：当AB与小圆相切时，OC⊥AB，
则AB=2AC=2
=2×4=8；
当AB过圆心时最长即为大圆的直径10．
则弦长AB的取值范围是8＜AB≤10．
故选C．
解：当AB与小圆相切时，OC⊥AB，则AB=2AC=2
| 25-9 |
当AB过圆心时最长即为大圆的直径10．
则弦长AB的取值范围是8＜AB≤10．
故选C．
点评：主要考查了直线与圆的位置关系，以及勾股定理和垂径定理的运用．要掌握同心圆的性质，并会利用垂径定理以及勾股定理解题．
练习册系列答案
天天练口算系列答案
相关题目
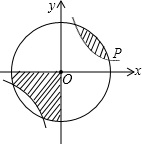如图，以点O为圆心的圆与反比例函数的图象相交，若其中一个交点P的坐标为（5，1），则图中两块阴影部分的面积和为
12、如图，以点P为圆心的圆弧与x轴交于A，B两点，点P的坐标为（4，2），点A的坐标为（2，0），则点B的坐标为
如图是以点O为圆心的半圆，AB是半圆的一条弦，延长OB与过点A的直线交于点C，AB=BC=OB．
如图，以点O为圆心的两个同心圆，当大圆的弦AB与小圆相切时弦长AB=8，则这两个同心圆所形成的圆环的面积是